
分析 (Ⅰ)x2+y2-2x+4y-m=0,整理得:(x-1)2+(y+2)2=m+5,根据点P(m,-2)在该圆的外部,建立不等式,即可求m的取值范围;
(Ⅱ)依题意假设直线l存在,其方程为x-y+p=0,N是弦AB的中点,利用|ON|=|AN|,从而得出结论.
解答 解:(I)∵x2+y2-2x+4y-m=0,
∴整理得:(x-1)2+(y+2)2=m+5.
由m+5>0得:m>-5.…(2分)
∵点P(m,-2)在该圆的外部,
∴(m-1)2+(-2+2)2>m+5.
∴m2-3m-4>0.
∴m>4或m<-1.
又∵m>-5,
∴m的取值范围是(-5,-1)∪(4,+∞).…(4分)
(II)当m=4时,圆C的方程为(x-1)2+(y+2)2=9.…(5分)
如图:依题意假设直线l存在,其方程为x-y+p=0,N是弦AB的中点.…(6分)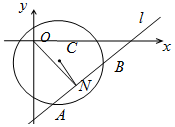
∴CN的方程为y+2=-(x-1).
联立l的方程可解得N的坐标为$(-\frac{p+1}{2}\;,\;\frac{p-1}{2}\;)$.…(7分)
∵原点O在以AB为直径的圆上,
∴|ON|=|AN|.
∴$\sqrt{{{(-\frac{p+1}{2}-0)}^2}+{{(\frac{p-1}{2}-0)}^2}}=\sqrt{{3^2}-|CN{|^2}}=\sqrt{9-{{(\frac{|3+p|}{{\sqrt{2}}})}^2}}$.
化简得:p2+3p-4=0,解得:p=-4或1.…(11分)
∴l的方程为x-y-4=0或x-y+1=0.…(12分)
点评 本题主要考查求圆的切线方程,直线和圆的位置关系应用,考查两点间距离公式的运用,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
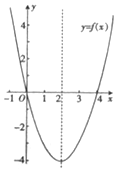 已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )
已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
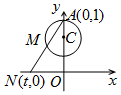 如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )| A. | 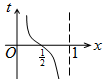 | B. | 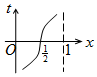 | C. | 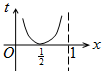 | D. | 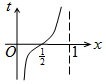 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | S<2014 | B. | S<2015 | C. | S<2016 | D. | S<2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | b<c<a | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com