
【题目】如图,在四棱锥![]() 中,PA⊥底面ABCD,BC∥AD,AB⊥BC,
中,PA⊥底面ABCD,BC∥AD,AB⊥BC,![]() ,
,![]() ,M是PD的中点.
,M是PD的中点.
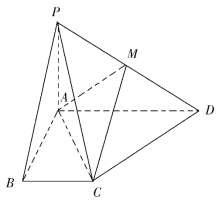
(1)求证:CM∥平面PAB;
(2)求二面角![]() 的余弦值.
的余弦值.
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
是否需要志愿 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人中,需要志愿帮助的老年人的比例?说明理由.
P | 0.0 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.用X表示抽取的3人中睡眠充足的员工人数,求随机变量X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90后从事互联网行业岗位分布条形图,则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.


A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的![]()
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,四分位数是指把一组数由小到大排列并分成四等份,处于三个分割点位置的数值为![]() ,
,![]() ,
,![]() ,其中
,其中![]() 是这组数的中位数,
是这组数的中位数,![]() 和
和![]() 分别可看作这组数被
分别可看作这组数被![]() 分成的前后两组数的中位数.利用四分位数可以绘制统计学中的箱形图:先找出一组数的最大值、最小值和三个四分位数
分成的前后两组数的中位数.利用四分位数可以绘制统计学中的箱形图:先找出一组数的最大值、最小值和三个四分位数![]() ;然后连接
;然后连接![]() 和
和![]() 画出“箱子”,中位数
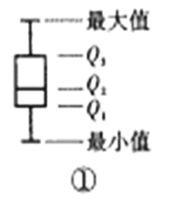
画出“箱子”,中位数![]() 在“箱子”中间;再将最大值和最小值与箱子相连接(如图①).某老师绘制了一次数学小测验中甲、乙、丙三个班级学生得分的箱形图(如图②),根据该图判断下列说法错误的是( )
在“箱子”中间;再将最大值和最小值与箱子相连接(如图①).某老师绘制了一次数学小测验中甲、乙、丙三个班级学生得分的箱形图(如图②),根据该图判断下列说法错误的是( )
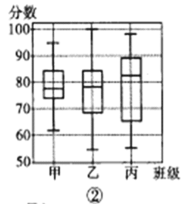
A.三个班级中,甲班分数的方差最小
B.三个班级中,乙班分数的极差最大
C.丙班得分低于80的学生人数多于得分高于80的学生人数
D.若每班有42个学生,则三个班级的第11名中,丙班的分数最高
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com