
【题目】某教研部门对本地区甲、乙、丙三所学校高三年级进行教学质量抽样调查,甲、乙、丙三所学校高三年级班级数量(单位:个)如下表所示。研究人员用分层抽样的方法从这三所学校中共抽取6个班级进行调查.
学校 | 甲 | 乙 | 丙 |
数量 | 4 | 12 | 8 |
(1)求这6个班级中来自甲、乙、丙三所学校的数量;
(2)若在这6个班级中随机抽取2个班级做进一步调查,
①列举出所有可能的抽取结果;
②求这2个班级来自同一个学校的概率.
【答案】(1)1,3,2;(2)①见解析②![]()
【解析】
(1)由题意,可得样本容量与总体中的个体数的比![]() ,进而可求解甲乙丙三所学校的数量,得到答案;
,进而可求解甲乙丙三所学校的数量,得到答案;
(2)设6个班级来自甲、乙、丙三所学校的样本分别为:甲;乙1,乙2,乙3;丙1,丙2利用列举法求得基本事件的总数,利用古典概型及其概率的计算公式,即可求解.
(1)因为样本容量与总体中的个体数的比是![]() ,
,
所以样本中包含三所学校的个体数量分别是![]() ,
,![]() ,
,![]() ,
,
所以这6个班级来自甲、乙、丙三所学校的数量分别为1,3,2.
(2)设6个班级来自甲、乙、丙三所学校的样本分别为:甲;乙1,乙2,乙3;丙1,丙2.
“抽取2个班级”所有可能结果有:{甲,乙1},{甲,乙2},{甲,乙3},{甲,丙1},{甲,丙2},{乙1,乙2},{乙1,乙3},{乙1,丙1},{乙1,丙2},{乙2,乙3},{乙2,丙1},{乙2,丙2},{乙3,丙1},{乙3,丙2},{丙1,丙2},共15个,
记事件![]() :“抽取的2个班级来自同一个学校”,则事件
:“抽取的2个班级来自同一个学校”,则事件![]() 的所有可能结果有:{乙1,乙2},{乙1,乙3},{乙2,乙3},{丙1,丙2},共4个,
的所有可能结果有:{乙1,乙2},{乙1,乙3},{乙2,乙3},{丙1,丙2},共4个,
所以![]() ,即这2个班级来自同一个学校的概率为
,即这2个班级来自同一个学校的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,已知矩形![]() 所在平面与半圆弧
所在平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是半圆弧
是半圆弧![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
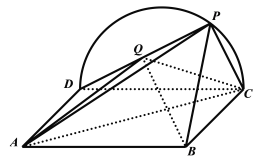
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,当三棱锥
,当三棱锥![]() 的体积最大且二面角
的体积最大且二面角![]() 的平面角的大小为
的平面角的大小为![]() 时,试确定
时,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点Q是圆![]() 上的动点,点
上的动点,点![]() ,若线段QN的垂直平分线MQ于点P.
,若线段QN的垂直平分线MQ于点P.
(I)求动点P的轨迹E的方程
(II)若A是轨迹E的左顶点,过点D(-3,8)的直线l与轨迹E交于B,C两点,求证:直线AB、AC的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
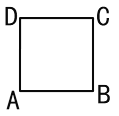
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为2个单位)的顶点
(边长为2个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到起点
个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到起点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )
A.21种B.22种C.25种D.27种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对在直角坐标系的第一象限内的任意两点![]() ,
,![]() 作如下定义:
作如下定义:![]() ,那么称点
,那么称点![]() 是点
是点![]() 的“上位点”,同时点
的“上位点”,同时点![]() 是点
是点![]() 的“下位点”.
的“下位点”.
(1)试写出点![]() 的一个“上位点”坐标和一个“下位点”坐标;
的一个“上位点”坐标和一个“下位点”坐标;
(2)设![]() 、
、![]() 、
、![]() 、
、![]() 均为正数,且点
均为正数,且点![]() 是点
是点![]() 的上位点,请判断点
的上位点,请判断点![]() 是否既是点
是否既是点![]() 的“下位点”又是点
的“下位点”又是点![]() 的“上位点”,如果是请证明,如果不是请说明理由;
的“上位点”,如果是请证明,如果不是请说明理由;
(3)设正整数![]() 满足以下条件:对任意实数
满足以下条件:对任意实数![]() ,总存在
,总存在![]() ,使得点
,使得点![]() 既是点
既是点![]() 的“下位点”,又是点
的“下位点”,又是点![]() 的“上位点”,求正整数
的“上位点”,求正整数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某公司生产线生产的某种产品中抽取![]() 件,测量这些产品的一项质量指标,由检测结果得如图所示的频率分布直方图:
件,测量这些产品的一项质量指标,由检测结果得如图所示的频率分布直方图:
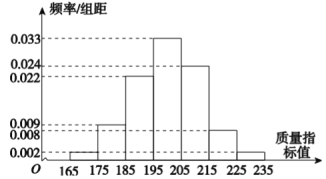
(Ⅰ)求这![]() 件产品质量指标的样本平均数
件产品质量指标的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)由直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)已知每件该产品的生产成本为![]() 元,每件合格品(质量指标值
元,每件合格品(质量指标值![]() )的定价为
)的定价为![]() 元;若为次品(质量指标值
元;若为次品(质量指标值![]() ),除了全额退款外且每件次品还须赔付客户
),除了全额退款外且每件次品还须赔付客户![]() 元。若该公司卖出
元。若该公司卖出![]() 件这种产品,记
件这种产品,记![]() 表示这件产品的利润,求
表示这件产品的利润,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com