
分析 确定直线AB方程为y=kx+1,该直线过定点(0,1).点M是直角三角形AOB斜边上的垂足,点M在以OC为直径的圆上运动,即可求点M的轨迹方程.
解答 解:设直线AB方程为y=kx+b,A(x1,y1),B(x2,y2),
将直线AB方程代入抛物线方程y=x2,
得x2-kx-b=0,
则x1+x2=k,x1x2=-b,
∴y1y2=b2,
∵OA⊥OB,∴kOA•kOB=-b=-1,b=1.
于是直线AB方程为y=kx+1,该直线过定点(0,1).
由题意知,点M是直角三角形AOB斜边上的垂足,
∴点M在以OC为直径的圆上运动,其运动轨迹方程为x2+(y-$\frac{1}{2}$)2=$\frac{1}{4}$(y≠0).
点评 本题考查直线与圆锥曲线的综合应用,考查学生分析解决问题的能力,考查运算求解能力,推理论证能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程$\frac{x}{y-2}=1$表示斜率为1,在y轴上的截距是2的直线 | |
| B. | △ABC的顶点坐标分别为A(0,3),B(-2,0),C(2,0),则中线AO的方程是x=0 | |
| C. | 到x轴距离为5的点的轨迹方程是y=5 | |
| D. | 曲线2x2-3y2-2x+m=0通过原点的充要条件是m=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
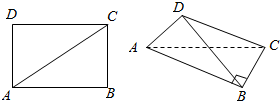 如图,在矩形ABCD中,AB=4,BC=3,沿对角线AC把矩形折成二面角D-AC-B,并且D点在平面ABC内的射影落在AB上.
如图,在矩形ABCD中,AB=4,BC=3,沿对角线AC把矩形折成二面角D-AC-B,并且D点在平面ABC内的射影落在AB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com