
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() 是
是![]() 上的一点,PE=2EC,
上的一点,PE=2EC, ![]() 为
为![]() 的中点.
的中点.
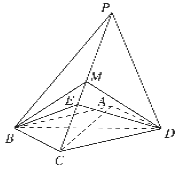
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明: ![]() 平面
平面![]() .
.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,△ABC是边长为2 ![]() 的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点.
的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点. 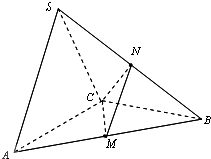
(1)证明:AC⊥SB;
(2)求三棱锥B﹣CMN的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明![]() ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.(3k+2)
B.(3k+4)
C.(3k+2)+(3k+3)
D.(3k+2)+(3k+3)+(3k+4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数(0,
有如下性质:如果常数t>0,那么该函数(0, ![]() ]上是减函数,在[
]上是减函数,在[ ![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知f(x)= ![]() ,g(x)=﹣x﹣2a,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域.
,g(x)=﹣x﹣2a,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域.
(2)对于(1)中的函数f(x)和函数g(x),若对于任意的x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=|log2x|的定义域为[ ![]() ,n](m,n为正整数),值域为[0,2],则满足条件的整数对(m,n)共有( )
,n](m,n为正整数),值域为[0,2],则满足条件的整数对(m,n)共有( )
A.1个
B.7个
C.8个
D.16个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某工厂从工程设计B到试生产H的工序流程图,方框上方的数字为这项工序所用的天数,则从工程设计到结束试生产需要的最短时间为( )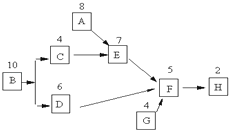
A.22天
B.23天
C.28天
D.以上都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(2,8),B(x1 , y1),C(x2 , y2)在抛物线 ![]() 上,△ABC的重心与此抛物线的焦点F重合(如图)
上,△ABC的重心与此抛物线的焦点F重合(如图)
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标;
(3)求BC所在直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com