
(14分)已知集合P={x|≤x≤2},函数y=log2(ax2-2x+2)的定义域是Q,
(1)若P∩Q≠φ,求实数a的取值范围.
(2)若方程log2(ax2-2x+2)=2在[,2]内有解,求实数a的取值范围。
解:(1)由已知Q={x| ax2-2x+2>0},若P∩Q≠φ,则说明在[,2]内至少有一个x值,使不等式ax2-2x+2>0成立,即在[,2]内至少有一个x值,使a> -成立,
令u= -,则只需a>umin,又u=-2(-)2+,当x∈[,2]时,从而u∈[-4, ],∴a>-4,∴a的取值范围是(-4,+∞).
(2)方程log2(ax2-2x+2)=2在[,2]内有解,则方程ax2-2x+2=4,即ax2-2x-2=0在[,2]内有解,故在[,2]内有x的值,使a=+ 成立。令u=+ .则
u=+ =2(+)2-,当x∈[,2]时,u∈[,12],∴a∈[,12].∴a的取值范围是[,12].


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:高中数学 来源: 题型:
|
| x2 |
| 4 |
|
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
已知关于![]() 的一元二次函数
的一元二次函数![]()
(Ⅰ)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作
为![]() 和
和![]() ,求函数
,求函数![]() 在区间[
在区间[![]() 上是增函数的概率;
上是增函数的概率;
(Ⅱ)设点(![]() ,
,![]() )是区域
)是区域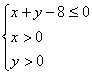 内的随机点,求函数
内的随机点,求函数![]() 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
已知关于![]() 的一元二次函数
的一元二次函数![]()
(Ⅰ)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作
为![]() 和
和![]() ,求函数
,求函数![]() 在区间[
在区间[![]() 上是增函数的概率;
上是增函数的概率;
(Ⅱ)设点(![]() ,
,![]() )是区域
)是区域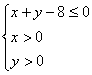 内的随机点,求函数
内的随机点,求函数![]() 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知集合![]()
![]() .对于A的一个子集S,若存在不大于
.对于A的一个子集S,若存在不大于![]() 的正整数m,使得对于S中的任意一对元素
的正整数m,使得对于S中的任意一对元素![]() ,都有
,都有![]() ,则称S具有性质P.
,则称S具有性质P.
(Ⅰ)当![]() 时,试判断集合
时,试判断集合![]() 和
和![]() 是否具有性质P?并说明理由.
是否具有性质P?并说明理由.
(Ⅱ)若![]() 时
时
若集合S具有性质P,那么集合![]() 是否一定具有性质P?并说明理由;
是否一定具有性质P?并说明理由;
若集合S具有性质P,求集合S中元素个数的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com