
【题目】如图所示在四棱锥![]() 中,下底面
中,下底面![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() ,
,![]() 为以
为以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() ,若点
,若点![]() 是线段
是线段![]() 上的中点.
上的中点.
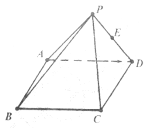
(1)证明![]() 平面
平面![]() .
.
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2019年国际篮联篮球世界杯,将于2019年在北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯,某大学从全校学生中随机抽取了120名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:

(1)根据上表说明,能否有![]() 的把握认为收看篮球世界杯赛事与性别有关?
的把握认为收看篮球世界杯赛事与性别有关?
(2)现从参与问卷调查的120名学生中,采用按性别分层抽样的方法选取6人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
(i)求男、女学生各选取多少人;
(ii)若从这6人中随机选取3人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到2名男生的概率.
附: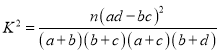 ,其中
,其中![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后得到如图的频率分
后得到如图的频率分
布直方图.

(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有学生1000人,试估计该校高一年级期中考试数学成绩不低于60分的人数.
(3)若从样本中数学成绩在![]() ,
,![]() 与
与![]() ,
,![]() 两个分数段内的学生中随机选取2名学生,试用列举法求这2名学生的数学成绩之差的绝对值大于10的槪率.
两个分数段内的学生中随机选取2名学生,试用列举法求这2名学生的数学成绩之差的绝对值大于10的槪率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的参数方程为
的参数方程为![]() (t为参数),以原点为极点,
(t为参数),以原点为极点,![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,曲线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,曲线![]() 关于
关于![]() 对称.
对称.
(1)求![]() 极坐标方程,
极坐标方程,![]() 直角坐标方程;
直角坐标方程;
(2)将![]() 向左平移4个单位长度,按照
向左平移4个单位长度,按照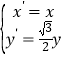 变换得到
变换得到![]() 与两坐标轴交于
与两坐标轴交于![]() 两点,
两点,![]() 为
为![]() 上任一点,求
上任一点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有员工45人,其中男员工27人,女员工18人.上级部门为了对该单位员工的工作业绩进行评估,采用按性别分层抽样的方法抽取5名员工进行考核.
(1)求抽取的5人中男、女员工的人数分别是多少;
(2)考核前,评估小组从抽取的5名员工中,随机选出3人进行访谈.求选出的3人中有1位男员工的概率;
(3)考核分笔试和答辩两项.5名员工的笔试成绩分别为78,85,89,92,96;结合答辩情况,他们的考核成绩分别为95,88,102,106,99.这5名员工笔试成绩与考核成绩的方差分别记为![]() ,试比较
,试比较![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有除颜色外形状大小完全相同的6个小球,其中有4个编号为1,2, 3, 4的红球,2个编号为A、B的黑球,现从中任取2个小球.;
(1)求所取2个小球都是红球的概率;
(2)求所取的2个小球颜色不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面四个命题:
①“直线![]() 平面
平面![]() 内所有直线”的充要条件是“
内所有直线”的充要条件是“![]() 平面
平面![]() ”;
”;
②“直线![]() 直线
直线![]() ”的充要条件是“
”的充要条件是“![]() 平行于
平行于![]() 所在的平面”;
所在的平面”;
③“直线![]() ,
,![]() 为异面直线”的充分不必要条件是“直线
为异面直线”的充分不必要条件是“直线![]() ,
,![]() 不相交”;
不相交”;
④“平面![]() 平面
平面![]() ”的必要不充分条件是“
”的必要不充分条件是“![]() 内存在不共线三点到
内存在不共线三点到![]() 的距离相等”.
的距离相等”.
其中正确命题的序号是____________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2018年第一季度五省GDP情况图,则下列描述中不正确的是( )
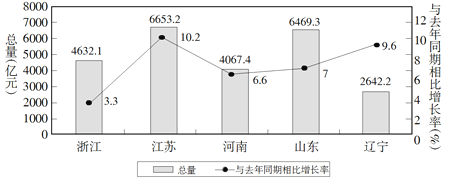
A. 与去年同期相比2018年第一季度五个省的GDP总量均实现了增长
B. 2018年第一季度GDP增速由高到低排位第5的是浙江省
C. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D. 去年同期河南省的GDP总量不超过4000亿元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() :
:![]() (
(![]() )的焦距相等,给出如下四个结论:
)的焦距相等,给出如下四个结论:
①![]() 和
和![]() 一定有交点;
一定有交点;
②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ;
;
④设![]() 与
与![]() 在第一象限内相交于点
在第一象限内相交于点![]() ,若
,若![]() ,则
,则![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com