
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(I)详见解析;(II)![]() ;(III)
;(III)![]() .
.
【解析】试题分析:
(1)利用题意证得![]() ,然后由线面平行的判断定理可得
,然后由线面平行的判断定理可得![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,利用平面向量的法向量可得二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)探索性问题,利用空间向量的结论可得在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,
此时![]() .
.
试题解析:
(Ⅰ)证明:设![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() .
.
因为![]() 为矩形,所以
为矩形,所以![]() 为
为![]() 的中点,
的中点,
在![]() 中,由已知
中,由已知![]() 为
为![]() 中点,
中点,
所以![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:取![]() 中点
中点![]() ,连接
,连接![]() .
.
因为![]() 是等腰三角形,
是等腰三角形, ![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
又因为平面![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() .
.
取![]() 中点
中点![]() ,连接
,连接![]() ,
,
由题设知四边形![]() 为矩形,
为矩形,
所以![]() ,
,
所以![]() .
.
如图建立空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则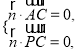 即
即![]()
令![]() ,则
,则![]() ,
, ![]() ,所以
,所以![]() .
.
平面![]() 的法向量为
的法向量为![]() ,
,
设![]() ,
, ![]() 的夹角为
的夹角为![]() ,所以
,所以![]() .
.
由图可知二面角![]() 为锐角,
为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)设![]() 是棱
是棱![]() 上一点,则存在
上一点,则存在![]() 使得
使得![]() .
.
因此点![]() ,
, ![]() ,
, ![]() .
.
由![]() ,即
,即![]() .
.
因为![]() ,所以在棱
,所以在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,
此时![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点R(x0 , y0)在D:y2=2px上,以R为切点的D的切线的斜率为 ![]() ,过Γ外一点A(不在x轴上)作Γ的切线AB、AC,点B、C为切点,作平行于BC的切线MN(切点为D),点M、N分别是与AB、AC的交点(如图).
,过Γ外一点A(不在x轴上)作Γ的切线AB、AC,点B、C为切点,作平行于BC的切线MN(切点为D),点M、N分别是与AB、AC的交点(如图).
(1)用B、C的纵坐标s、t表示直线BC的斜率;
(2)设三角形△ABC面积为S,若将由过Γ外一点的两条切线及第三条切线(平行于两切线切点的连线)围成的三角形叫做“切线三角形”,如△AMN,再由M、N作“切线三角形”,并依这样的方法不断作切线三角形…,试利用“切线三角形”的面积和计算由抛物线及BC所围成的阴影部分的面积T.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院逐步打开”,此消息在网上一石激起千层浪.各种说法不一而足,为了了解居民对“开放小区”认同与否,从[25,55]岁人群中随机抽取了n人进行问卷调查,得如下数据:
组数 | 分组 | 认同人数 | 认同人数占 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55) | 15 | 0.3 |
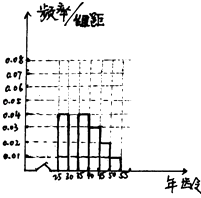
(1)完成所给频率分布直方图,并求n,a,p.
(2)若从[40,45),[45,50)两个年龄段中的“认同”人群中,按分层抽样的方法抽9人参与座谈会,然后从这9人中选2名作为组长,组长年龄在[40,45)内的人数记为ξ,求随机变量ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C1的参数方程为 ![]() ,(α为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+
,(α为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+ ![]() )=4
)=4 ![]() .
.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)设P为曲线C1上的动点,求点P到C2上点的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时生产内径为![]() 的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位:
的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位: ![]() ) ,
) ,
甲:25.44,25.43, 25.41,25.39,25.38
乙:25.41,25.42, 25.41,25.39,25.42.
从生产的零件内径的尺寸看、谁生产的零件质量较高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为y=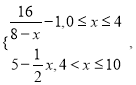 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(1≤a≤4)个单位的药剂,要使接下来的4天中能够持续有效净化,试求a的最小值(精确到0.1,参考数据: ![]() 取1.4).
取1.4).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为R,集合A={x| ![]() ≥0},B={x|﹣2≤x<0},则(RA)∩B=( )
≥0},B={x|﹣2≤x<0},则(RA)∩B=( )
A.(﹣1,0)
B.[﹣1,0)
C.[﹣2,﹣1]
D.[﹣2,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列![]() 个结论:
个结论:
①棱长均相等的棱锥一定不是六棱锥;
②函数![]() 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数;
③若函数![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④若函数![]() 满足条件
满足条件![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中正确的结论的序号是:______. (写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com