
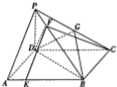
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.分析 (1)取AB中点H,以D为原点,DH为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能证明AC⊥DF.
(2)连结AC,BD,交于点O,由已知条件推导出EF∥OG,由此能证明EF∥平面BDG.
(3)利用向量法求出F到平面BEC的距离d=3t=3,三棱锥B-CEF的体积VB-CEF=VF-BEC.,由此能求出结果.
解答 证明:(1) 取AB中点H,以D为原点,DH为x轴,DC为y轴,DP为z轴,
取AB中点H,以D为原点,DH为x轴,DC为y轴,DP为z轴,
建立空间直角坐标系,
设P(0,0,4t),t>0,
由已知得A(2$\sqrt{6}$,-2$\sqrt{2}$,0),C(0,4$\sqrt{2}$,0),D(0,0,0),
B(2$\sqrt{6}$,2$\sqrt{2}$,0),F($\frac{\sqrt{6}}{2}$,$\frac{\sqrt{2}}{2}$,3t),
$\overrightarrow{AC}$=(-2$\sqrt{6}$,6$\sqrt{2}$,0),$\overrightarrow{DF}$=($\frac{\sqrt{6}}{2}$,$\frac{\sqrt{2}}{2}$,3t),
∴$\overrightarrow{AC}•\overrightarrow{DF}$=-6+6+0=0,
∴AC⊥DF.
(2)连结AC,BD,交于点O,
∵底面ABCD为菱形,∴O是AC中点,
∵G是PC中点,∴OG∥AP,
∵E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF,
∴EF∥AP,∴EF∥OG,
∵EF?平面BDG,OG?平面BDG,
∴EF∥平面BDG.
解:(3)$\overrightarrow{PA}$=(2$\sqrt{6}$,2$\sqrt{2}$,-4t),$\overrightarrow{PC}$=(0,4$\sqrt{2}$,-4t),
∵PA⊥PC,∴$\overrightarrow{PA}•\overrightarrow{PC}$=0+16-16t2=0,解得t=1,
∴F到平面BEC的距离d=3t=3,
∵∠ADC=120°,底面ABCD为菱形,AB=4AE=4$\sqrt{2}$,
∴BE=3$\sqrt{2}$,BC=4$\sqrt{2}$,
∴S△BEC=$\frac{1}{2}×3\sqrt{2}×4\sqrt{2}×sin120°$=6$\sqrt{3}$,
∴三棱锥B-CEF的体积VB-CEF=VF-BEC=$\frac{1}{3}×{S}_{△BEC}×d$=6$\sqrt{3}$.
点评 本题考查的知识点是直线与平面平行的证明,考查二面角的平面角及求法,建立空间坐标系,将空间夹角问题转化为向量夹角问题是解答的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{9}$ | B. | $-\frac{8}{9}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$或 2 | C. | $2\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
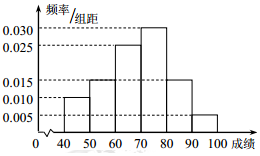 在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).| 文科生 | 理科生 | 合计 | |
| 获奖 | 5 | ||
| 不获奖 | |||
| 合计 | 200 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
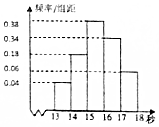 为调查运城市学生百米运动成绩,从该市学生中按照男女比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
为调查运城市学生百米运动成绩,从该市学生中按照男女比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | a=24 | b=6 | 30 |
| 不达标 | c=8 | d=12 | 20 |
| 合计 | 32 | 18 |
| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.625 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com