
【题目】有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
A.264B.72C.266D.274
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两名射箭选手最近100次射箭所得环数如下表所示.
甲选手100次射箭所得环数
环数 | 7 | 8 | 9 | 10 |
次数 | 15 | 24 | 36 | 25 |
乙选手100次射箭所得环数
环数 | 7 | 8 | 9 | 10 |
次数 | 10 | 20 | 40 | 30 |
以甲、乙两名射箭选手这100次射箭所得环数的频率作为概率,假设这两人的射箭结果相互独立.
(1)若甲、乙各射箭一次,所得环数分别为X,Y,分别求X,Y的分布列并比较![]() 的大小;
的大小;
(2)甲、乙相约进行一次射箭比赛,各射3箭,累计所得环数多者获胜.若乙前两次射箭均得10环,且甲第一次射箭所得环数为9,求甲最终获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,![]() 是以PF为底边的等腰三角形,PA平行于x轴,点
是以PF为底边的等腰三角形,PA平行于x轴,点![]() ,且点P在直线
,且点P在直线![]() 上运动.记点A的轨迹为C.
上运动.记点A的轨迹为C.
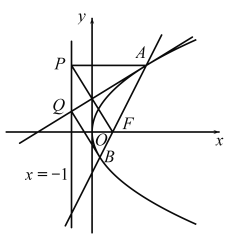
(1)求C的方程.
(2)直线AF与C的另一个交点为B,等腰![]() 底边的中线与直线
底边的中线与直线![]() 的交点为Q,试问
的交点为Q,试问![]() 的面积是否存在最小值?若存在,求出该值;若不存在,请说明理由.
的面积是否存在最小值?若存在,求出该值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的焦距为2,椭圆
)的焦距为2,椭圆![]() 的左右焦点分别为
的左右焦点分别为![]()
![]() ,过右焦点
,过右焦点![]() 作
作![]() 轴的垂线交椭圆于
轴的垂线交椭圆于![]()
![]() 两点,
两点,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 作直线交椭圆于
作直线交椭圆于![]()
![]() 两点,若△
两点,若△![]() 的内切圆的面积为
的内切圆的面积为![]() ,求△
,求△![]() 的面积;
的面积;
(3)已知![]() ,
,![]() 为圆上一点(
为圆上一点(![]() 在
在![]() 轴右侧),过
轴右侧),过![]() 作圆的切线交椭圆
作圆的切线交椭圆![]() 于
于![]()
![]() 两点,试问△
两点,试问△![]() 的周长是否为一定值?若是,求出该定值,若不是,请说明理由.
的周长是否为一定值?若是,求出该定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个简单图中两两相邻的t个项点称为一个团,与其余每个顶点均相邻的顶点称为中心点.给定整数![]() 及满足
及满足![]() 的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为
的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为![]() .
.
(1)证明:![]() ;
;
(2)若在图G中再添加一条边就存在k+1团,求图G的中心点个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强学生体质,合肥一中组织体育社团,某班级有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团.
(1)求这4人中恰有1人参加篮球社团的概率;
(2)用![]() ,
,![]() 分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为
分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为![]() 和
和![]() 之差的绝对值,求随机变量X的分布列与数学期望
之差的绝对值,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com