
【题目】有下列四个命题:(1)一定存在直线![]() ,使函数
,使函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称;(2)不等式:
对称;(2)不等式:![]() 的解集为
的解集为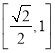 ;(3)已知数列
;(3)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,则数列
,则数列![]() 一定是等比数列;(4)过抛物线
一定是等比数列;(4)过抛物线![]() 上的任意一点
上的任意一点![]() 的切线方程一定可以表示为
的切线方程一定可以表示为![]() .则正确命题的序号为_________________.
.则正确命题的序号为_________________.
【答案】(3)(4)
【解析】
(1)中,可利用函数![]() 与
与![]() 关于
关于![]() 轴对称进行判定;
轴对称进行判定;
(2)中,利用反三角函数的定义,直接求出符合条件的解集,即可判定;
(3)利用![]() 求得数列的通项公式,即可判定;
求得数列的通项公式,即可判定;
(4)利用直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 有且仅有一个交点,即可判定.
有且仅有一个交点,即可判定.
对于(1)中,由函数![]() 与
与![]() 关于
关于![]() 轴对称,而函数
轴对称,而函数![]() 的图像与函数
的图像与函数![]() 的图象向上平移的幅度不一样,所以它们不关于
的图象向上平移的幅度不一样,所以它们不关于![]() 轴对称,所以找不到这样的直线满足题意,所以不正确;
轴对称,所以找不到这样的直线满足题意,所以不正确;
对于(2)中,因为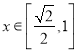 时,
时,![]() ,
,
所以不等式![]() 的解集为
的解集为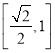 是不正确的;
是不正确的;
对于(3)中,由![]() ,当
,当![]() 时,
时,![]() ,满足上式,
,满足上式,
所以数列![]() 是一个等比数列,
是一个等比数列,
所以数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,则数列
,则数列![]() 一定是等比数列是正确的;
一定是等比数列是正确的;
对于(4)中,由直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 有且仅有一个交点,所以过抛物线
有且仅有一个交点,所以过抛物线![]() 上的任意一点
上的任意一点![]() 的切线方程一定可以表示为
的切线方程一定可以表示为![]() 是正确的.
是正确的.
故答案为:(3)(4).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题中:①若“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②若“![]() ,
,![]() ”,则实数
”,则实数![]() 的取值范围是
的取值范围是![]() ;
;
③已知平面![]() 、
、![]() 、
、![]() ,直线
,直线![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④函数![]() 的所有零点存在区间是
的所有零点存在区间是![]() .
.
其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现定义:设![]() 是非零实常数,若对于任意的
是非零实常数,若对于任意的![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“关于的
为“关于的![]() 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的![]() 偶型函数”在区间
偶型函数”在区间![]() 上单调递增,求证在区间
上单调递增,求证在区间![]() 上单调递减
上单调递减
(3)设定义域为![]() 的“关于
的“关于![]() 的偶型函数”
的偶型函数”![]() 是奇函数,若
是奇函数,若![]() ,请猜测
,请猜测![]() 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在开展学习强国的活动中,某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有4名男教师、1名女教师,非党员学习组有2名男教师、2名女教师,高三数学组计划从两个学习组中随机各选2名教师参加学校的挑战答题比赛.
(1)求选出的4名选手中恰好有一名女教师的选派方法数;
(2)记X为选出的4名选手中女教师的人数,求X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对函数![]() 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
![]() 函数在
函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]() 点
点![]() 是函数图象的一个对称中心;
是函数图象的一个对称中心;
![]() 函数图象关于直线
函数图象关于直线![]() 对称;
对称;
![]() 存在常数
存在常数![]() ,使
,使![]() 对一切实数x均成立,
对一切实数x均成立,
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为降低雾霾等恶劣气候对居民的影响,某公司研发了一种新型防雾霾产品.每一台新产品在进入市场前都必须进行两种不同的检测,只有两种检测都合格才能进行销售,否则不能销售.已知该新型防雾霾产品第一种检测不合格的概率为![]() ,第二种检测不合格的概率为
,第二种检测不合格的概率为![]() ,两种检测是否合格相互独立.
,两种检测是否合格相互独立.
(1)求每台新型防雾霾产品不能销售的概率;
(2)如果产品可以销售,则每台产品可获利40元;如果产品不能销售,则每台产品亏损80元(即获利![]() 元).现有该新型防雾霾产品3台,随机变量
元).现有该新型防雾霾产品3台,随机变量![]() 表示这3台产品的获利,求
表示这3台产品的获利,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,底面ABCD是直角梯形,
平面ABCD,底面ABCD是直角梯形,![]() ,
,![]() ,
,![]() ,O是AD的中点.
,O是AD的中点.
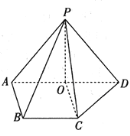
(1)在线段PA上找一点E,使得![]() 平面PCD,并证明;
平面PCD,并证明;
(2)在(1)的条件下,若![]() ,求平面OBE与平面POC所成的锐二面角的余弦值.
,求平面OBE与平面POC所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com