
【题目】已知![]() ,
, ![]() 。
。
(1)写出![]() 的解析式与定义域;
的解析式与定义域;
(2)画出函数![]() 的图像;
的图像;
(3)试讨论方程![]() 的根的个数。
的根的个数。
【答案】(1)定义域![]()
 (2)见解析(3)
(2)见解析(3)![]() 时,方程有一解;
时,方程有一解; ![]() 时,方程有两解;
时,方程有两解; ![]() 时,方程无解。
时,方程无解。
【解析】试题分析:(1)根据表达式,得出函数f(x)的定义域是(﹣2,+∞),将H(x)化成分段函数的形式.
(2)得到函数y=H(x﹣1)+2的分段表达式,进而可以作出它的图象;
(3)根据图象可以得到,当m=2或m≥10时,直线y=m与函数y=H(x﹣1)+2图象有且仅有一个公共点;当2<m<10时,直线y=m与函数y=H(x﹣1)+2图象有两个公共点;当m<2时,直线y=m与函数y=H(x﹣1)+2图象没有公共点.由此则不难得出方程根的个数了.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
, 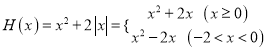
(2)![]() =
= ,
,
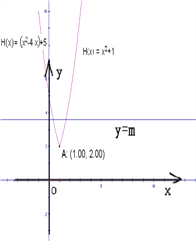
(3)在同一坐标系里作出直线y=m,观察它与函数y=H(x)图象的交点的个数,可得
①当m=2或m≥10时,直线y=m与函数y=H(x﹣1)+2图象有且仅有一个公共点;②当2<m<10时,直线y=m与函数y=H(x﹣1)+2图象有两个公共点;③当m<2时,直线y=m与函数y=H(x﹣1)+2图象没有一个公共点
由此可得:当m∈{2}∪[10,+∞)时,方程H(x﹣1)+2=m有且仅有一个实数根;
![]() 时,方程有一解;
时,方程有一解;
![]() 时,方程有两解;
时,方程有两解; ![]() 时,方程无解。
时,方程无解。


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3+
x3+![]() x2+
x2+![]() x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格![]() (元)与时间
(元)与时间![]() (天)组成有序数对
(天)组成有序数对![]() ,点
,点![]() 落在图中的两条线段上.
落在图中的两条线段上.
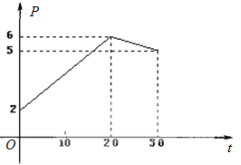
该股票在30天内的日交易量![]() (万股)与时间
(万股)与时间![]() (天)的部分数据如下表所示:
(天)的部分数据如下表所示:
第 | 4 | 10 | 16 | 22 |
| 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该股票每股交易价格![]() (元)与时间
(元)与时间![]() (天)所满足的函数关系式;
(天)所满足的函数关系式;
(2)根据表中数据,写出日交易量![]() (万股)与时间
(万股)与时间![]() (天)的一次函数关系式;
(天)的一次函数关系式;
(3)用![]() (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出![]() 关于
关于![]() 的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列{n∈N+}.
求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明:![]() 为等比数列;
为等比数列;
(3)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过定点P(-2,1)作直线l分别与x、y轴交于A、B两点,
(1)求经过点P且在两坐标轴上的截距相等的直线l方程.
(2)求使![]() 面积为4时的直线l方程。
面积为4时的直线l方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com