
甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为l,2,3,4,5,6点),所得点数分别记为 ,则
,则 的概率为
的概率为
A. | B. | C. | D. |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:单选题
从甲口袋摸出一个红球的概率是 ,从乙口袋中摸出一个红球的概率是
,从乙口袋中摸出一个红球的概率是 ,则
,则 是( )
是( )
| A.2个球不都是红球的概率 | B.2个球都是红球的概率 |
| C.至少有一个红球的概率 | D.2个球中恰好有1个红球的概率 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
对于给定的实数 ,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),记出现向上的点数分别为
,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),记出现向上的点数分别为 ,如果
,如果 是偶数,则把
是偶数,则把 乘以2后再减去2;如果
乘以2后再减去2;如果 是奇数,则把
是奇数,则把 除以2后再加上2,这样就可得到一个新的实数
除以2后再加上2,这样就可得到一个新的实数 ,对
,对 仍按上述方法进行一次操作,又得到一个新的实数
仍按上述方法进行一次操作,又得到一个新的实数 .当
.当 时,甲获胜,否则乙获胜.若甲获胜的概率为
时,甲获胜,否则乙获胜.若甲获胜的概率为 ,则
,则 的值不可能是
的值不可能是
| A.0 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
从装有2只红球和2只黑球的口袋内任取2个球,那么互斥而不对立的两个事件是
| A.至少有1只黑球与都是黑球 | B.至少有1只黑球与都是红球 |
| C.至少有1只黑球与至少有1只红球 | D.恰有1只黑球与恰有2只黑球 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
抛掷一骰子,观察出现的点数,设事件A为“出现1点”,事件B为“出现2点”.已知P(A)=P(B)= ,则“出现1点或2点”的概率为( ).
,则“出现1点或2点”的概率为( ).
A. | B.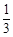 | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知一颗粒子等可能地落入如右图所示的四边形 内的任意位置,如果通过大量的实验发现粒子落入△
内的任意位置,如果通过大量的实验发现粒子落入△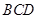 内的频率稳定在
内的频率稳定在 附近,那么点
附近,那么点 和点
和点 到时直线
到时直线 的距离之比约为( )
的距离之比约为( )
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com