
【题目】已知数列{an}的前n项和为Sn,a1=1,an>0,Sn2=an+12﹣λSn+1,其中λ为常数.
(1)证明:Sn+1=2Sn+λ;
(2)是否存在实数λ,使得数列{an}为等比数列,若存在,求出λ;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在,λ=1
【解析】
(1)利用已知条件通过an+1=Sn+1﹣Sn,推出Sn+1(Sn+1﹣2Sn﹣λ)=0,然后证明:Sn+1=2Sn+λ;.
(2)求出数列的通项公式,利用数列是等比数列,求解即可.
(1)证明:∵an+1=Sn+1﹣Sn,![]() ,
,
∴![]() ,
,
∴Sn+1(Sn+1﹣2Sn﹣λ)=0,
∴an>0,∴Sn+1>0,
∴Sn+1﹣2Sn﹣λ=0;
∴Sn+1 = 2Sn+λ
(2)解:∵Sn+1=2Sn+λ,Sn=2Sn﹣1+λ(n≥2),
相减得:an+1=2an(n≥2),∴{an}从第二项起成等比数列,
∵S2=2S1+λ即a2+a1=2a1+λ,
∴a2=1+λ>0得λ>﹣1,
∴an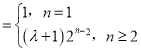 ,
,
若使{an}是等比数列
则![]() ,∴2(λ+1)=(λ+1)2,
,∴2(λ+1)=(λ+1)2,
∴λ=1经检验得符合题意.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
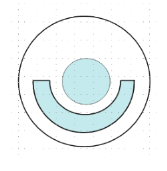
【题目】2019年4月10日21时整,全球六地(上海和台北、布鲁塞尔、圣地亚哥、东京和华盛顿同时召开新闻发布会,宣布人类首次利用虚拟射电望远镜,成功捕获世界上首张黑洞图像,公布的照片展示了一个中心为黑色的明亮环状结构,看上去有点像个橙色的甜甜圈,其黑色部分是黑洞投下的“阴影”,明亮部分是绕黑洞高速旋转的吸积盘.某同学作了一张黑洞示意图,如图所示,由两个同心圆和半个同心圆环构成圆及圆环的半径从内到外依次为2,3,4,5个单位在图中随机任取一点,则该点取自阴影的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放40多年来,城乡居民生活从解决温饱的物质需求为主逐渐转变到更多元化的精神追求,消费结构明显优化.下图给出了1983~2017年部分年份我国农村居民人均生活消费支出与恩格尔系数(恩格尔系数是食品支出总额占个人消费支出总额的比重)统计图.对所列年份进行分析,则下列结论错误的是( )
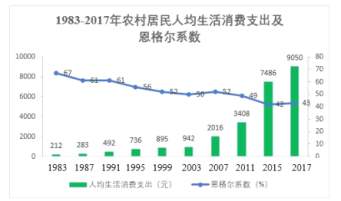
A.农村居民人均生活消费支出呈增长趋势
B.农村居民人均食品支出总额呈增长趋势
C.2011年至2015年农村居民人均生活消费支出增长最快
D.2015年到2017年农村居民人均生活消费支出增长比率大于人均食品支出总额增长比率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现有效利用扶贫资金,增加贫困村民的收入,扶贫工作组结合某贫困村水质优良的特点,决定利用扶贫资金从外地购买甲、乙、丙三种鱼苗在鱼塘中进行养殖试验,试验后选择其中一种进行大面积养殖,已知鱼苗甲的自然成活率为0.8.鱼苗乙,丙的自然成活率均为0.9,且甲、乙、丙三种鱼苗是否成活相互独立.
(1)试验时从甲、乙,丙三种鱼苗中各取一尾,记自然成活的尾数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)试验后发现乙种鱼苗较好,扶贫工作组决定购买![]() 尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新冠病毒肺炎(COVID﹣19)疫情在武汉爆发,并以极快的速度在全国传播开来.因该病毒暂无临床特效药可用,因此防控难度极大.湖北某地防疫防控部门决定进行全面入户排查4类人员:新冠患者、疑似患者、普通感冒发热者和新冠密切接触者,过程中排查到一户5口之家被确认为新冠肺炎密切接触者,按要求进一步对该5名成员逐一进行核糖核酸检测,若出现阳性,则该家庭定义为“感染高危户”,设该家庭每个成员检测呈阳性的概率相同均为![]() ,且相互独立,该家庭至少检测了4人才能确定为“感染高危户”的概率为
,且相互独立,该家庭至少检测了4人才能确定为“感染高危户”的概率为![]() ,当
,当![]() 时,
时,![]() 最大,此时
最大,此时![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,AB=AC=![]() ,BC=AA1=2,O,M分别为BC,AA1的中点.
,BC=AA1=2,O,M分别为BC,AA1的中点.

(1)求证:OM∥平面CB1A1;
(2)求点M到平面CB1A1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱柱![]() 的底面边长为2,侧棱长为4,过点
的底面边长为2,侧棱长为4,过点![]() 作平面
作平面![]() 与正四棱柱的三条侧棱
与正四棱柱的三条侧棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,且
,且![]() ,若多面体
,若多面体![]() 和多面体
和多面体![]() 的体积比为3∶5,则截面
的体积比为3∶5,则截面![]() 的周长为_________.
的周长为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com