
【题目】设椭圆C:![]() 的一个顶点与抛物线:
的一个顶点与抛物线:![]() 的焦点重合,
的焦点重合,![]() 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率![]() ,过椭圆右焦点
,过椭圆右焦点![]() 的直线l与椭圆C交于M、N两点.
的直线l与椭圆C交于M、N两点.
(1)求椭圆C的方程;
(2)是否存在直线l,使得![]() ,若存在,求出直线l的方程;若不存在,说明理由;
,若存在,求出直线l的方程;若不存在,说明理由;
【答案】(1)![]() ;(2)y=±
;(2)y=±![]() (x﹣1)
(x﹣1)
【解析】
(1)根据抛物线的焦点求得![]() 的值,利用离心率和
的值,利用离心率和![]() 列方程,解方程后可求得
列方程,解方程后可求得![]() 的值,进而求得椭圆方程.(2)当斜率为零时,验证
的值,进而求得椭圆方程.(2)当斜率为零时,验证![]() ,不符合题意.当斜率不为零时,设出直线的方程,联立直线的方程和椭圆的方程,写出韦达定理,计算
,不符合题意.当斜率不为零时,设出直线的方程,联立直线的方程和椭圆的方程,写出韦达定理,计算![]() ,可求得直线的斜率,由此求得直线的方程.
,可求得直线的斜率,由此求得直线的方程.
解:(I)由已知得b![]() ,
,
又e![]() ,
,
∴a2=3,
∴椭圆C的方程为:![]() ;;
;;
(II)若直线l的斜率为0,则![]() 3(舍去);
3(舍去);
若直线斜率不为0,设直线l的方程为:x=my+1,
代入椭圆C的方程,消去y整理得:
(3+2m2)y2+4my﹣4=0,
设M(x1,y1),N(x2,y2),
则有:y1+y2![]() ,y1y2
,y1y2![]() ,
,
又∵x1=my1+1,x2=my2+1,
∴![]() x1x2+y1y2
x1x2+y1y2
=(my1+1)(my2+1)+y1y2
=(1+m2)y1y2+m(y1+y2)+1
=(1+m2)(![]() )+m(
)+m(![]() )+1
)+1
=﹣1,
解得m=±![]() ,
,
∴直线l方程为:y=±![]() (x﹣1);
(x﹣1);


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】某大型企业针对改善员工福利的![]() ,
,![]() ,
,![]() 三种方案进行了问卷调查,调查结果如下:
三种方案进行了问卷调查,调查结果如下:
支持 | 支持 | 支持 | |
35岁以下的人数 | 200 | 400 | 800 |
35岁及以上的人数 | 100 | 100 | 400 |
(1)从所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,已知从支持
人,已知从支持![]() 方案的人中抽取了6人,求
方案的人中抽取了6人,求![]() 的值.
的值.
(2)从支持![]() 方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对平面区域![]() ,用
,用![]() 表示属于
表示属于![]() 的所有整点(即
的所有整点(即![]() 平面上坐标
平面上坐标![]() 都是整数的点)的个数.若
都是整数的点)的个数.若![]() 表示由曲线
表示由曲线![]() 和两直线
和两直线![]() 所围成的区域(包括边界);
所围成的区域(包括边界);![]() 表示由曲线
表示由曲线![]() 和两直线
和两直线![]() 所围成的区域(包括边界).则
所围成的区域(包括边界).则![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)令![]() ,讨论
,讨论![]() 的单调性.
的单调性.
(3)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数的底数,
为自然对数的底数,![]() …).
…).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级的一次月考成绩中随机抽取了 50名学生的成绩(满分100分,且抽取的学生成绩都在![]() 内),按成绩分为
内),按成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,得到如图所示的频率分布直方图.
五组,得到如图所示的频率分布直方图.

(1)用分层抽样的方法从月考成绩在![]() 内的学生中抽取6人,求分别抽取月考成绩在
内的学生中抽取6人,求分别抽取月考成绩在![]() 和
和![]() 内的学生多少人;
内的学生多少人;
(2)在(1)的前提下,从这6名学生中随机抽取2名学生进行调查,求月考成绩在![]() 内至少有1名学生被抽到的概率.
内至少有1名学生被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》 是我国古代的天文学和数学著作。其中一个问题的大意为:一年有二十四个节气(如图),每个节气晷长损益相同(即物体在太阳的照射下影子长度的增加量和减少量相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:ー丈等于十尺,一尺等于十寸),则立冬节气的晷长为( )
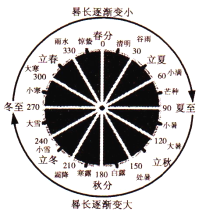
A. 九尺五寸 B. 一丈五寸 C. 一丈一尺五寸 D. 一丈六尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知第二小组的频数是40.

(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数;
(3)求这两个班参赛学生的成绩的中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com