
【题目】孔子曰:温故而知新.数学学科的学习也是如此.为了调查数学成绩与及时复习之间的关系,某校志愿者展开了积极的调查活动:从高三年级640名学生中按系统抽样抽取40名学生进行问卷调查,所得信息如下:
数学成绩优秀(人数) | 数学成绩合格(人数) | |
及时复习(人数) | 20 | 4 |
不及时复习(人数) | 10 | 6 |
(1)张军是640名学生中的一名,他被抽中进行问卷调查的概率是多少(用分数作答);
(2)根据以上数据,运用独立性检验的基本思想,研究数学成绩与及时复习的相关性.
参考公式: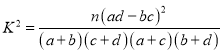 ,其中
,其中![]() 为样本容量
为样本容量
临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】为满足人们的阅读需求,图书馆设立了无人值守的自助阅读区,提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况,数据统计如下(单位:本).
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
(1)根据统计数据估计文学类图书分类正确的概率;
(2)根据统计数据估计图书分类错误的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】郴州某超市计划按月订购一种饮料,每天进货量相同,进货成本每瓶6元,售价每瓶8元,未售出的饮料降价处理,以每瓶3元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种饮料一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种饮料的利润为Y(单位:元),当六月份这种饮料一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月1日新修订的个税法正式实施,规定:公民全月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额.此项税款按下表分段累计计算(预扣):
全月应缴纳所得额 | 税率 |
不超过3000元的部分 |
|
超过3000元至12000元的部分 |
|
超过12000元至25000元的部分 |
|
国家在实施新个税时,考虑到纳税人的实际情况,实施了《个人所得税税前专项附加扣税暂行办法》,具体如下表:
项目 | 每月税前抵扣金额(元) | 说明 |
子女教育 | 1000 | 一年按12月计算,可扣12000元 |
继续教育 | 400 | 一年可扣除4800元,若是进行技能职业教育或者专业技术职业资格教育一年可扣除3600元 |
大病医疗 | 5000 | 一年最高抵扣金额为60000元 |
住房贷款利息 | 1000 | 一年可扣除12000元,若夫妻双方在同一城市工作,可以选择一方来扣除 |
住房租金 | 1500/1000/800 | 扣除金额需要根据城市而定 |
2000 | 一年可扣除24000元,若不是独生子女,子女平均扣除.赡养老人年龄需要在60周岁及以上 |
老李本人为独生子女,家里有70岁的老人需要赡养,有一个女儿正读高三,他每月还需缴纳住房贷款2734元.若2019年11月老李工资,薪金所得为20000元,按照《个人所得税税前专项附加扣税暂行办法》,则老李应缴纳税款(预扣)为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

A.①反映建议(2),③反映建议(1)B.①反映建议(1),③反映建议(2)
C.②反映建议(1),④反映建议(2)D.④反映建议(1),②反映建议(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,试用列举法表示集合
,试用列举法表示集合![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com