
【题目】已知函数![]() ,
,![]() .
.
(I)讨论![]() 的单调性;
的单调性;
(II)若![]() 恒成立,证明:当
恒成立,证明:当![]() 时,
时,![]() .
.
(III)在(II)的条件下,证明:![]() .
.
【答案】I.见解析;Ⅱ.见解析;III 见解析.
【解析】
I:对函数求导,分类讨论导函数的正负,进而得到单调性;Ⅱ:通过分类讨论可得到a=1,根据![]() ,得到:
,得到:![]() ,进而得到结果; III:通过讨论函数的单调性得到
,进而得到结果; III:通过讨论函数的单调性得到![]() ,进而得到:
,进而得到:![]() ,由Ⅱ知
,由Ⅱ知![]() 两式相乘得到结果.
两式相乘得到结果.
I.![]()
若![]() ,f(x)在
,f(x)在![]() 上递增;
上递增;
若a>0,当![]() 时,
时,![]() ,f(x)单调递增;
,f(x)单调递增;
当![]() 时,
时,![]() 单调递减。
单调递减。
Ⅱ.由I知,若a≤0,f(x)在(0,+![]() )上递增,又f(l)=0,故f(x)≤0不恒成立
)上递增,又f(l)=0,故f(x)≤0不恒成立
若a>1,当![]() 时,f(x)递减,f(x)>f(1)=0,不合题意。
时,f(x)递减,f(x)>f(1)=0,不合题意。
若0<a<1,当![]() 时,f(x)递增,f(x)>f(l)=0.不合题意。
时,f(x)递增,f(x)>f(l)=0.不合题意。
若a=1.f(x)在(0,1)上递增.在(1,+![]() )上递减,f(x)≤f(1)=0,合题意。
)上递减,f(x)≤f(1)=0,合题意。
故a=1,且![]() (当且仅当x=1时取 “=”)
(当且仅当x=1时取 “=”)
当0<x1<x2时,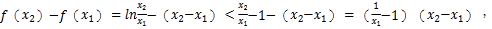
所以![]()
III.![]()
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,g(x)单调递减。
,g(x)单调递减。
![]()
![]() ①
①
由(Ⅱ)知![]() (当且仅当x=1时取 “=”)........... ②
(当且仅当x=1时取 “=”)........... ②
两个不等式的等号不能同时取到,故得到:
①![]() ②得
②得![]()
即![]() ,
,
![]()


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】江夏一中高二年级计划假期开展历史类班级研学活动,共有6个名额,分配到历史类5个班级(每个班至少0个名额,所有名额全部分完).
(1)共有多少种分配方案?
(2)6名学生确定后,分成A、B、C、D四个小组,每小组至少一人,共有多少种方法?
(3)6名学生来到武汉火车站.火车站共设有3个“安检”入口,每个入口每次只能进1个旅客,求6人进站的不同方案种数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
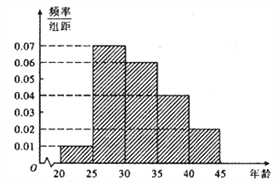 (2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
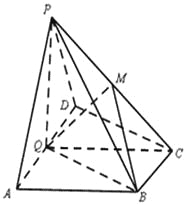
【题目】如图,已知三棱锥![]() 中,平面
中,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,BD=3,AD=1,AC=BC,M为线段AB的中点.
,BD=3,AD=1,AC=BC,M为线段AB的中点.
(Ⅰ)求证:![]() 平面ACD;
平面ACD;
(Ⅱ)求异面直线MD与BC所成角的余弦值;
(Ⅲ)求直线MD与平面ACD所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 为棱
为棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)若二面角![]() 大小为
大小为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,点
的中点,点![]() 为上底面的中心,过
为上底面的中心,过![]() ,
,![]() ,
,![]() 三点的平面把正方体分为两部分,其中含
三点的平面把正方体分为两部分,其中含![]() 的部分为
的部分为![]() ,不含
,不含![]() 的部分为
的部分为![]() ,连结
,连结![]() 和
和![]() 的任一点
的任一点![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() 的最大值为
的最大值为

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过两点
经过两点![]() ,
,![]() ,且圆心
,且圆心![]() 在直线
在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,点
两点,点![]() 为圆
为圆![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 交
交![]() 轴于
轴于![]() 、
、![]() 点.当点
点.当点![]() 变化时,以
变化时,以![]() 为直径的圆
为直径的圆![]() 是否经过圆
是否经过圆![]() 内一定点?请证明你的结论.
内一定点?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com