
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2017年种植的一批试验紫甘薯在温度升高时6组死亡的株数:

经计算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数, ![]() .
.
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (结果精确到
(结果精确到![]() );
);
(2)若用非线性回归模型求得![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ,且相关指数为
,且相关指数为![]() .
.
(i)试与(1)中的回归模型相比,用![]() 说明哪种模型的拟合效果更好;
说明哪种模型的拟合效果更好;
(ii)用拟合效果好的模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
, ![]() ,……,
,……, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 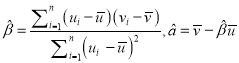 ;相关指数为:
;相关指数为: 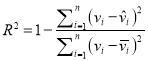 .
.
【答案】(Ⅰ) ![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】试题分析:(1)利用回归方程的公式,求得线性回归方程为: ![]() =6.6x139.4;(2)(i)
=6.6x139.4;(2)(i)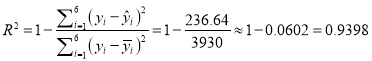 ,因为0.9398<0.9522,所以回归方程
,因为0.9398<0.9522,所以回归方程![]() 比线性回归方程
比线性回归方程![]() =6.6x138.6拟合效果更好;(ii)当温度
=6.6x138.6拟合效果更好;(ii)当温度![]() 时,
时, ![]() ,即当温度为35C时该批紫甘薯死亡株数为190.
,即当温度为35C时该批紫甘薯死亡株数为190.
试题解析:
(Ⅰ)由题意得, 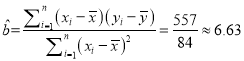
∴![]() 336.6326=139.4,
336.6326=139.4,
∴![]() 关于
关于![]() 的线性回归方程为:
的线性回归方程为: ![]() =6.6x139.4.
=6.6x139.4.
(注:若用![]() 计算出
计算出![]() ,则酌情扣1分)
,则酌情扣1分)
(Ⅱ) (i)线性回归方程![]() =6.6x138.6对应的相关系数为:
=6.6x138.6对应的相关系数为:
 ,
,
因为0.9398<0.9522,
所以回归方程![]() 比线性回归方程
比线性回归方程![]() =6.6x138.6拟合效果更好.
=6.6x138.6拟合效果更好.
(ii)由(i)知,当温度![]() 时,
时,
![]() ,
,
即当温度为35C时该批紫甘薯死亡株数为190.


科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎![]() 疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,小王同学发现,每个国家在疫情发生的初期,由于认识不足和措施不到位,感染人数都会出现快速的增长.下表是小王同学记录的某国连续8天每日新型冠状病毒感染确诊的累计人数.
疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,小王同学发现,每个国家在疫情发生的初期,由于认识不足和措施不到位,感染人数都会出现快速的增长.下表是小王同学记录的某国连续8天每日新型冠状病毒感染确诊的累计人数.
日期代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累计确诊人数 | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
为了分析该国累计感染人数的变化趋势,小王同学分别用两种模型:①![]() ,②
,②![]() 对变量
对变量![]() 和
和![]() 的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差
的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差![]() ):经过计算得
):经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
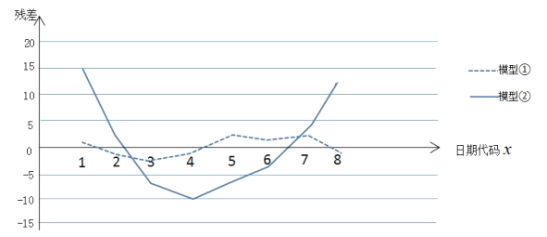
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由;
(2)根据(1)问选定的模型求出相应的回归方程(系数均保留一位小数);
(3)由于时差,该国截止第9天新型冠状病毒感染确诊的累计人数尚未公布.小王同学认为,如果防疫形势没有得到明显改善,在数据公布之前可以根据他在(2)问求出的回归方程来对感染人数作出预测,那么估计该地区第9天新型冠状病毒感染确诊的累计人数是多少.
附:回归直线的斜率和截距的最小二乘估计公式分别为: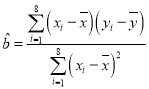 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了节能减排,发展低碳经济,我国政府从2001年起就通过相关扶植政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
中国新能源汽车产销情况一览表 | ||||
新能源汽车产量 | 新能源汽车销量 | |||
产量(万辆) | 比上年同期增长( | 销量(万辆) | 比上年同期增长( | |
2018年3月 | 6.8 | 105 | 6.8 | 117.4 |
4月 | 8.1 | 117.7 | 8.2 | 138.4 |
5月 | 9.6 | 85.6 | 10.2 | 125.6 |
6月 | 8.6 | 31.7 | 8.4 | 42.9 |
7月 | 9 | 53.6 | 8.4 | 47.7 |
8月 | 9.9 | 39 | 10.1 | 49.5 |
9月 | 12.7 | 64.4 | 12.1 | 54.8 |
10月 | 14.6 | 58.1 | 13.8 | 51 |
11月 | 17.3 | 36.9 | 16.9 | 37.6 |
1-12月 | 127 | 59.9 | 125.6 | 61.7 |
2019年1月 | 9.1 | 113 | 9.6 | 138 |
2月 | 5.9 | 50.9 | 5.3 | 53.6 |
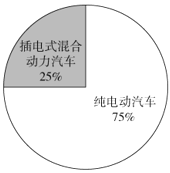
2019年2月份新能源汽车销量结构图
根据上述图表信息,下列结论错误的是( )
A.2018年4月份我国新能源汽车的销量高于产量
B.2017年3月份我国新能源汽车的产量不超过3.4万辆
C.2019年2月份我国插电式混合动力汽车的销量低于1万辆
D.2017年我国新能源汽车总销量超过70万辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,且椭圆经过点
的左、右焦点,且椭圆经过点![]() 和点
和点![]() ,其中
,其中![]() 为椭圆的离心率.
为椭圆的离心率.

(1)求椭圆的方程;
(2)过点![]() 的直线
的直线![]() 椭圆于另一点
椭圆于另一点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .若
.若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
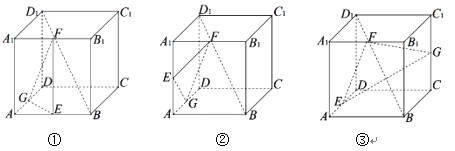
【题目】如图,在下列三个正方体![]() 中,
中,![]() 均为所在棱的中点,过
均为所在棱的中点,过![]() 作正方体的截面.在各正方体中,直线
作正方体的截面.在各正方体中,直线![]() 与平面
与平面![]() 的位置关系描述正确的是
的位置关系描述正确的是
A. ![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②③
的有且只有②③
B. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有①
的有且只有①
C. .![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②
的有且只有②
D. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有③
的有且只有③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,
倍,![]() 为侧棱
为侧棱![]() 上的点.
上的点.
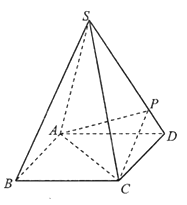
(1)求证:![]() ;
;
(2)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(3)在(2)的条件下,侧棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() .若存在,求
.若存在,求![]() 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD, PA=AD=2,E,F分别为PA,AB的中点,且DF⊥CE.
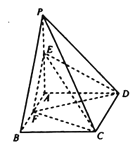
(1)求AB的长;
(2)求直线CF与平面DEF所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com