
【题目】如图在四面体ABCD中,若截面PQMN是正方形,则在下列命题中正确的有 .(填上所有正确命题的序号)
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④异面直线PM与BD所成的角为45°.
【答案】①③④
【解析】解:在四面体ABCD中,∵截面PQMN是正方形,∴PQ∥MN,PQ平面ACD,MN平面ACD,∴PQ∥平面ACD.
∵平面ACB∩平面ACD=AC,∴PQ∥AC,可得AC∥平面PQMN.
同理可得BD∥平面PQMN,BD∥PN.
∵PN⊥PQ,∴AC⊥BD.
由BD∥PN,
∴∠MPN是异面直线PM与BD所成的角,且为45°.
由上面可知:BD∥PN,PQ∥AC.
∴![]()
而AN≠DN,PN=MN,
∴BD≠AC.
综上可知:①③④都正确.
所以答案是:①③④.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用和异面直线及其所成的角的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() (
(![]() ),设
),设![]() 为圆
为圆![]() 与
与![]() 轴负半轴的交点,过点
轴负半轴的交点,过点![]() 作圆
作圆![]() 的弦
的弦![]() ,并使弦
,并使弦![]() 的中点恰好落在
的中点恰好落在![]() 轴上.
轴上.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)延长![]() 交曲线
交曲线![]() 于点
于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 交于点
交于点![]() ,试判断以点
,试判断以点![]() 为圆心,线段
为圆心,线段![]() 长为半径的圆与直线
长为半径的圆与直线![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ),四点
),四点![]() ,
, ![]() ,
, 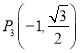 ,
, 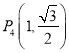 中恰有三点在椭圆上.
中恰有三点在椭圆上.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 不经过
不经过![]() 点且与
点且与![]() 相交于
相交于![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]() ,证明:
,证明: ![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的直线的方程:
(1)经过两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0;
(2)经过两条直线2x+y﹣8=0和x﹣2y+1=0的交点,且平行于直线4x﹣3y﹣7=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x>0时,函数f(x)的解析式为![]() .
.
(1)求当x<0时函数f(x)的解析式;
(2)用定义证明f(x)在(0,+∞)上的是减函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com