
【题目】已知函数![]() ,其中
,其中![]() 是函数
是函数![]() 的导数,
的导数, ![]() 为自然对数的底数,
为自然对数的底数, ![]() (
(![]() ,
,![]() ).
).
(Ⅰ)求![]() 的解析式及极值;
的解析式及极值;
(Ⅱ)若![]() ,求
,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是各项均为正数的等差数列.
是各项均为正数的等差数列.
(1)若![]() ,且
,且![]() 成等比数列,求数列
成等比数列,求数列![]() 的通项公式
的通项公式![]() ;
;
(2)在(1)的条件下,数列![]() 的前
的前![]() 和为
和为![]() ,设
,设![]() ,若对任意的
,若对任意的![]() ,不等式
,不等式![]() 恒成立,求突数
恒成立,求突数![]() 的最小值:
的最小值:
(3)若数列![]() 中有两项可以表示位某个整数
中有两项可以表示位某个整数![]() 的不同次冪,求证:数列
的不同次冪,求证:数列![]() 中存在无穷多项构成等比数列.
中存在无穷多项构成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一枚质地均匀的硬币向上抛掷三次,下列两个事件中,是对立事件的是( )
A.事件![]() :“恰有两次正面向上”,事件
:“恰有两次正面向上”,事件![]() :“恰有两次反面向上”
:“恰有两次反面向上”
B.事件![]() :“恰有两次正面向上”,事件
:“恰有两次正面向上”,事件![]() :“恰有一次正面向上”
:“恰有一次正面向上”
C.事件![]() :“至少有一次正面向上”,事件
:“至少有一次正面向上”,事件![]() :“至多一次正面向上”
:“至多一次正面向上”
D.事件![]() :“至少有一次正面向上”,事件
:“至少有一次正面向上”,事件![]() :“恰有三次反面向上”
:“恰有三次反面向上”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,智能手机的更新换代极其频繁和快速,而青少年对新事物的追求更是强烈,为了调查大学生更换手机的时间,现对某大学中的大学生使用一部手机的年限进行了问卷调查,并从参与调查的大学生中抽取了男生、女生各![]() 人进行抽样分析,制成如下的频率分布直方图.
人进行抽样分析,制成如下的频率分布直方图.

(1)根据频率分布直方图,估计男大学生使用手机年限的中位数和女大学生使用手机年限的众数;
(2)根据频率分布直方图,求出男大学生和女大学生使用手机年限的平均值,并分析比较男大学生和女大学生哪个群体更换手机的频率更高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点M(0,-1),直线l经过点N(2,1)且与椭圆C相交于A,B两点(异于点M),记直线MA的斜率为![]() ,直线MB的斜率为
,直线MB的斜率为![]() ,证明
,证明![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
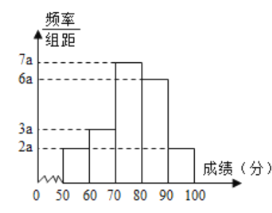
(1)求频率分布直方图中![]() 的值;
的值;
(2)估计总体中成绩落在![]() 中的学生人数;
中的学生人数;
(3)根据频率分布直方图估计![]() 名学生数学考试成绩的众数,中位数.
名学生数学考试成绩的众数,中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为正项等比数列,a1+a2=6,a3=8.
(1)求数列{an}的通项公式an;
(2)若bn=![]() ,且{bn}前n项和为Tn,求Tn.
,且{bn}前n项和为Tn,求Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() ,若直线
,若直线![]() 的图像上存在点
的图像上存在点![]() ,使得
,使得![]() 成立,则说直线
成立,则说直线![]() 是“
是“![]() 型直线”.给出下列直线:
型直线”.给出下列直线:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() (常数
(常数![]() )
)
其中代表“![]() 型直线”的序号是___________.(要求写出所有
型直线”的序号是___________.(要求写出所有![]() 型直线的序号)
型直线的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com