
 与向量
与向量 的夹角记为α,则α
的夹角记为α,则α 的概率为( )
的概率为( )



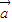 的情况数目;进而根据向量的数量积公式可得cosα=
的情况数目;进而根据向量的数量积公式可得cosα=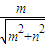 ,由余弦函数的性质可得若α
,由余弦函数的性质可得若α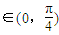 ,则
,则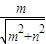 <
<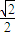 ,对其变形化简可得m>n,由列举法可得其情况数目,由等可能事件的概率公式计算可得答案.
,对其变形化简可得m>n,由列举法可得其情况数目,由等可能事件的概率公式计算可得答案.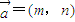 的情况有6×6=36种,
的情况有6×6=36种,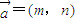 ,向量
,向量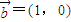 ,
,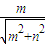 ,
,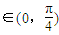 ,则
,则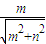 <
<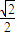 ,
,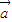 的坐标可以为:(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5),共有15种情况;
的坐标可以为:(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5),共有15种情况;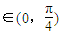 的概率为
的概率为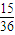 =
=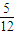 ,
,

科目:高中数学 来源:2011-2012学年山西省四校高三第三次联考考试理科数学试卷 题型:选择题
连续投掷两次骰子得到的点数分别为 ,向量
,向量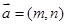 与向量
与向量 的夹角记为
的夹角记为 ,则
,则
 的概率为
的概率为
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2010年北京八中大兴分校高考数学模拟试卷(理科)(解析版) 题型:选择题
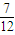



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com