
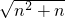 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: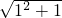 <1+1,不等式成立.
<1+1,不等式成立.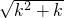 <k+1,则当n=k+1时,
<k+1,则当n=k+1时,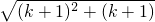 =
=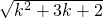 <
<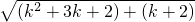 =
=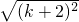 =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立. 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(1)当n=1时, ![]() <1+1,不等式成立.
<1+1,不等式成立.
(2)假设当n=k(k∈N*)时,不等式成立,即![]() <k+1,则当n=k+1时,
<k+1,则当n=k+1时, ![]() <
<![]() ,
,
∴当n=k+1时,不等式成立.
上述证法( )
A.过程全部正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
查看答案和解析>>
科目:高中数学 来源:2011年《龙门亮剑》高三数学(理科)一轮复习:第一章第6节 集合、常用逻辑用语、推理证明(解析版) 题型:选择题
 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: <1+1,不等式成立.
<1+1,不等式成立. <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
< =
=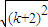 =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:6.7 数学归纳法2(理科)(解析版) 题型:选择题
 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: <1+1,不等式成立.
<1+1,不等式成立. <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
< =
= =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:6.7 数学归纳法1(理科)(解析版) 题型:选择题
 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: <1+1,不等式成立.
<1+1,不等式成立. <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
<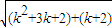 =
= =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.查看答案和解析>>
科目:高中数学 来源:2011年《龙门亮剑》高三数学(文科)一轮复习:第1章第6节(人教AB通用)(解析版) 题型:选择题
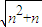 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: <1+1,不等式成立.
<1+1,不等式成立.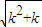 <k+1,则当n=k+1时,
<k+1,则当n=k+1时,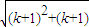 =
=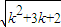 <
<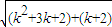 =
=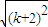 =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com