
【题目】在以坐标原点为极点,![]() 轴的正半轴为极轴建立的极坐标系中,曲线
轴的正半轴为极轴建立的极坐标系中,曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程:
的极坐标方程:![]() .
.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 交
交![]() 轴于点
轴于点![]() (不是原点),过点
(不是原点),过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于A,B两个不同的点,求
于A,B两个不同的点,求![]() 的取值范围.
的取值范围.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】已知定义域为[0,1]的函数f(x)同时满足以下三个条件:
①对任意的x∈[0,1],总有f(x)≥0;
②f(1)=1;
③当x1,x2∈[0,1],且x1+x2∈[0,1]时,f(x1+x2)≥f(x1)+f(x2)成立.称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知f(x)为“友谊函数”,求f(0)的值;
(2)函数g(x)=2x-1在区间[0,1]上是否为“友谊函数”?请给出理由;
(3)已知f(x)为“友谊函数”,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f[f(x0)]=x0,求证: f(x0)=x0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 分别是定义在
分别是定义在![]() 上的偶函数和奇函数,且
上的偶函数和奇函数,且![]() .
.
(1)求函数![]() ,
,![]() 的解析式;
的解析式;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)设![]() ,若函数
,若函数![]() 与
与![]() 的图象有且只有一个公共点,求
的图象有且只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆的极坐标方程为:ρ2-4![]() ρcos(θ-
ρcos(θ-![]() )+6=0.
)+6=0.
(1)将极坐标方程化为普通方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2019年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图,给出下列4个结论
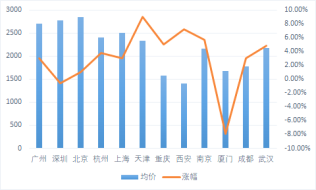
其中结论正确的是( )
A.深圳的变化幅度最小,北京的平均价格最高;
B.深圳和厦门往返机票的平均价格同去年相比有所下降;
C.平均价格从高到低位于前三位的城市为北京,深圳,广州;
D.平均价格的涨幅从高到低位于前三位的城市为天津,西安,上海.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax3-3ax,g(x)=bx2-ln x(a,b∈R),已知它们在x=1处的切线互相平行.
(1)求b的值;
(2)若函数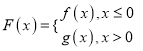 且方程F(x)=a2有且仅有四个解,求实数a的取值范围.
且方程F(x)=a2有且仅有四个解,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com