
【题目】已知函数f(x)=2|x+2|﹣|x+1|,无穷数列{an}的首项a1=a.
(1)如果an=f(n)(n∈N*),写出数列{an}的通项公式;
(2)如果an=f(an﹣1)(n∈N*且n≥2),要使得数列{an}是等差数列,求首项a的取值范围;
(3)如果an=f(an﹣1)(n∈N*且n≥2),求出数列{an}的前n项和Sn .
【答案】
(1)解:∵函数f(x)=2|x+2|﹣|x+1|=  ,
,
又n≥1且n∈N*,∴an=f(n)=n+3
(2)解:如果{an}是等差数列,则an﹣an﹣1=d,an=an﹣1+d,
由f(x)知一定有an=an﹣1+3,公差d=3.
当a1≥﹣1时,符合题意.
当﹣2≤a1≤﹣1时,a2=3a1+5,由a2﹣a1=3得3a1+5﹣a1=3,得a1=﹣1,a2=2.
当a1≤﹣2时,a2=﹣a1﹣3,由a2﹣a1=3得﹣a1﹣3﹣a1=3,得a1=﹣3,此时a2=0.
综上所述,可得a的取值范围是a≥﹣1或a=﹣3
(3)解:当a≥﹣1时,an=f(an﹣1)=an﹣1+3,∴数列{an}是以a为首项,公差为3的等差数列, ![]() .
.
当﹣2≤a≤﹣1时,a2=3a1+5=3a+5≥﹣1,∴n≥3时,an=an﹣1+3.∴n=1时,S1=a.n≥2时, ![]()
又S1=a也满足上式,∴ ![]() (n∈N*)
(n∈N*)
当a≤﹣2时,a2=﹣a1﹣3=﹣a﹣3≥﹣1,∴n≥3时,an=an﹣1+3.∴n=1时,S1=a.n≥2时, ![]()
又S1=a也满足上式,∴ ![]() (n∈N*).
(n∈N*).
综上所述:Sn= 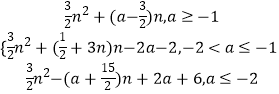
【解析】(1)化简函数f(x)为分段函数,然后求出an=f(n)=n+3.(2)如果{an}是等差数列,求出公差d,首项,然后求解a的范围.(3)当a≥﹣1时,求出前n项和,当﹣2≤a≤﹣1时,当a≤﹣2时,分别求出n项和即可.


科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[m,n]上的函数,记F(x)=f(x)﹣(ax+b),|F(x)|的最大值为M(a,b).若存在m≤x1<x2<x3≤n,满足|F(x1)|=M(a,b),F(x2)=﹣F(x1).F(x3)=F(x1),则称一次函数y=ax+b是f(x)的“逼近函数”,此时的M(a,b)称为f(x)在[m,n]上的“逼近确界”.
(1)验证:y=4x﹣1是g(x)=2x2 , x∈[0,2]的“逼近函数”;
(2)已知f(x)= ![]() ,x∈[0,4],F(0)=F(4)=﹣M(a,b).若y=ax+b是f(x)的“逼近函数”,求a,b的值;
,x∈[0,4],F(0)=F(4)=﹣M(a,b).若y=ax+b是f(x)的“逼近函数”,求a,b的值;
(3)已知f(x)= ![]() ,x∈[0,4]的逼近确界为
,x∈[0,4]的逼近确界为 ![]() ,求证:对任意常数a,b,M(a,b)≥
,求证:对任意常数a,b,M(a,b)≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( ) 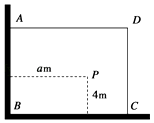
A.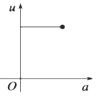
B.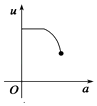
C.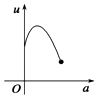
D.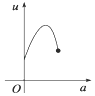
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C是平面内到直线l1:x=﹣1和直线l2:y=1的距离之积等于常数k2(k>0)的点的轨迹,下列四个结论:
①曲线C过点(﹣1,1);
②曲线C关于点(﹣1,1)成中心对称;
③若点P在曲线C上,点A、B分别在直线l1、l2上,则|PA|+|PB|不小于2k;
④设P0为曲线C上任意一点,则点P0关于直线l1:x=﹣1,点(﹣1,1)及直线f(x)对称的点分别为P1、P2、P3 , 则四边形P0P1P2P3的面积为定值4k2;其中,
所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40 ![]() 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ= ![]() ,0°<θ<90°)且与点A相距10
,0°<θ<90°)且与点A相距10 ![]() 海里的位置C. (Ⅰ)求该船的行驶速度(单位:海里/小时);
海里的位置C. (Ⅰ)求该船的行驶速度(单位:海里/小时);
(Ⅱ)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则( )
A.乙盒中黑球不多于丙盒中黑球
B.乙盒中红球与丙盒中黑球一样多
C.乙盒中红球不多于丙盒中红球
D.乙盒中黑球与丙盒中红球一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”问此人第4天和第5天共走了( )
A.60里
B.48里
C.36里
D.24里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax3﹣bex(a∈R,b∈R),且f(x)在x=0处的切线与x﹣y+3=0垂直.
ax3﹣bex(a∈R,b∈R),且f(x)在x=0处的切线与x﹣y+3=0垂直.
(1)若函数f(x)在[ ![]() ,1]存在单调递增区间,求实数a的取值范围;
,1]存在单调递增区间,求实数a的取值范围;
(2)若f′(x)有两个极值点x1 , x2 , 且x1<x2 , 求a的取值范围;
(3)在第二问的前提下,证明:﹣ ![]() <f′(x1)<﹣1.
<f′(x1)<﹣1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com