
【题目】![]() 年,某省将实施新高考,
年,某省将实施新高考,![]() 年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用
年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用![]() 模式,其中语文、数学、外语三科为必考科目,满分各
模式,其中语文、数学、外语三科为必考科目,满分各![]() 分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物
分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物![]() 门科目中自选
门科目中自选![]() 门参加考试(
门参加考试(![]() 选
选![]() ),每科目满分
),每科目满分![]() 分.为了应对新高考,某高中从高一年级
分.为了应对新高考,某高中从高一年级![]() 名学生(其中男生
名学生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分层抽样的方法从中抽取n名学生进行调查.
人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含女生![]() 人,求n的值及抽取到的男生人数;
人,求n的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的![]() 列联表,请将下面的列联表补充完整,并判断是否有
列联表,请将下面的列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“历史” | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
(3)在抽取到的![]() 名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出
名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出![]() 名女生,了解女生对“历史”的选课意向情况,在这
名女生,了解女生对“历史”的选课意向情况,在这![]() 名女生中再抽取
名女生中再抽取![]() 人,求这
人,求这![]() 人中选择“历史”的人数为
人中选择“历史”的人数为![]() 人的概率.
人的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: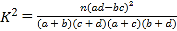 ,其中
,其中![]() )
)
【答案】(1)![]() ;男生人数为:55人(2)填表见解析;没有95%的把握认为选择科目与性别有关,详见解析(3)
;男生人数为:55人(2)填表见解析;没有95%的把握认为选择科目与性别有关,详见解析(3)![]()
【解析】
(1)根据分层抽样比进行计算即可;
(2)根据(1)所给的数据,可以完成![]() 列联表,再根据题中所给的公式求出
列联表,再根据题中所给的公式求出![]() 的值,再结合参考数据进行判断得出结论即可;
的值,再结合参考数据进行判断得出结论即可;
(3)根据分层抽样比进行计算求出6名女生中选择物理和历史的人数,根据古典概型的计算公式,结合列举法进行求解即可.
解:(1)由题意,根据分层抽样的方法,可得![]() ,解得
,解得![]() ,
,
所以男生人数为:![]() 人.
人.![]() ,男生人数为:55人;.
,男生人数为:55人;.
(2)由(1)中得知;男生人数为55人,选择“历史”的有10人,因此选择“物理”的有![]() 人;男生人数为45人,选择“物理”的有30人,因此选择“历史”的有
人;男生人数为45人,选择“物理”的有30人,因此选择“历史”的有![]() 人,
人,
所以![]() 列联表为:
列联表为:
选择“物理” | 选择“历史” | 总计 | |
男生 | 45 | 10 | 55 |
女生 | 30 | 15 | 45 |
总计 | 75 | 25 | 100 |
![]() .
.
所以没有95%的把握认为选择科目与性别有关.
(3)选择物理与选择历史的女生人数的比为2:1,所以按分层抽样有人选择物理,设为a,b,c,d,2人选择历史,设为A,B,..
从中选取3人,共有20种选法,可表示为abc,abd,acd,
bcd,abA,abB,acA,acB,adA,adB,bcA,bcB,bdA,bdB,cdA,cdB,aAB,bAB,cAB,dAB.
其中有2人选择历史的有aAB,bAB,cAB,dAB4种,
故这3人中有2人选择历史的概率为![]()


科目:高中数学 来源: 题型:
【题目】某口罩厂一年中各月份的收入、支出情况如图所示(单位:万元,下列说法中错误的是(注:月结余=月收入一月支出)( )
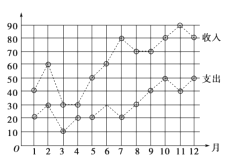
A.上半年的平均月收入为45万元B.月收入的方差大于月支出的方差
C.月收入的中位数为70D.月结余的众数为30
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分类是对垃圾进行有效处置的一种科学管理方法.太原市为推进这项工作的实施,开展了“垃圾分类进小区”的评比活动.现有甲、乙两个小区采取不同的宣传与倡导方式对各自小区居民进行了有关垃圾分类知识的培训,并参加了评比活动,评委会随机从两个小区各选出20户家庭进行评比打分,每户成绩满分为100分,评分后得到如下茎叶图.
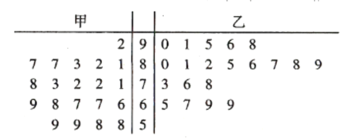
(1)依茎叶图判断哪个小区的平均分高?
(2)现从甲小区不低于80分的家庭中随机抽取两户,求分数为87的家庭至少有一户被抽中的概率;
(3)如果规定分数不低于85分的家庭为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为得分是否优秀与小区宣传培训方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为得分是否优秀与小区宣传培训方式有关?”
甲 | 乙 | 合计 | |
优秀 |
|
| |
不优秀 |
|
| |
合计 |
参考公式和数据: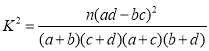 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,
,![]() ,点
,点![]() 为坐标平面内的一点,且
为坐标平面内的一点,且![]() ,
,![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,![]() ,
,![]() 是椭圆
是椭圆![]() 上两个不同的点,直线
上两个不同的点,直线![]() ,
,![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() ,且
,且![]() .证明:直线
.证明:直线![]() 恒过定点,并求出该定点的坐标,
恒过定点,并求出该定点的坐标,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月1日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房货款利息、住房租金、赡养老人.某单位有老年员工140人,中年员工180人,青年员工80人,现采用分层抽样的方法,从该单位员工中抽取20人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如下:
员工\人数\专项 | 子女教育 | 继续教育 | 大病医疗 | 住房贷款利息 | 住房租金 | 赡养老人 |
老员工 | 4 | 0 | 2 | 2 | 0 | 3 |
中年员工 | 8 | 2 | 1 | 5 | 1 | 8 |
青年员工 | 1 | 2 | 0 | 1 | 2 | 1 |
(Ⅰ)在抽取的20人中,老年员工、中年员工、青年员工各有多少人;
(Ⅱ)从上表享受住房货款利息专项扣除的员工中随机选取2人,求选取2人都是中年员工的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是无穷数列,若存在正整数k,使得对任意
是无穷数列,若存在正整数k,使得对任意![]() ,均有
,均有![]() ,则称
,则称![]() 是间隔递增数列,k是
是间隔递增数列,k是![]() 的间隔数,下列说法正确的是( )
的间隔数,下列说法正确的是( )
A.公比大于1的等比数列一定是间隔递增数列
B.已知![]() ,则
,则![]() 是间隔递增数列
是间隔递增数列
C.已知![]() ,则
,则![]() 是间隔递增数列且最小间隔数是2
是间隔递增数列且最小间隔数是2
D.已知![]() ,若
,若![]() 是间隔递增数列且最小间隔数是3,则
是间隔递增数列且最小间隔数是3,则![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com