
已知首项为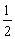 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若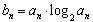 ,数列{bn}的前n项和Tn,求满足不等式
,数列{bn}的前n项和Tn,求满足不等式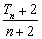 ≥
≥ 的最大n值.
的最大n值.
(I)an=a1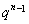 =(
=( )n;(Ⅱ)n的最大值为4.
)n;(Ⅱ)n的最大值为4.
【解析】
试题分析:(I){an}是一等比数列,且a1=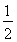 .设等比数列{an}的公比为q,由S1+a1,S2+a2,S3+a3成等差数列,可得一个含公比q的方程,解这个方程便得公比q,从而得数列{an}通项公式.
.设等比数列{an}的公比为q,由S1+a1,S2+a2,S3+a3成等差数列,可得一个含公比q的方程,解这个方程便得公比q,从而得数列{an}通项公式.
(Ⅱ)由题设及(I)可得:bn=anlog2an=-n?( )n,由等差数列与等比数列的积或商构成的新数列,求和时用错位相消法.用错位相消法可求得
)n,由等差数列与等比数列的积或商构成的新数列,求和时用错位相消法.用错位相消法可求得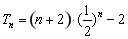 ,变形得
,变形得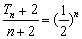 ≥
≥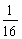 ,解这个不等式得n≤4,从而得 n的最大值.
,解这个不等式得n≤4,从而得 n的最大值.
试题解析:(I)设等比数列{an}的公比为q,由题知 a1=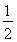 ,
,
又∵ S1+a1,S2+a2,S3+a3成等差数列,
∴ 2(S2+a2)=S1+a1+S3+a3,
变形得S2-S1+2a2=a1+S3-S2+a3,即得3a2=a1+2a3,
∴ 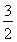 q=
q= +q2,解得q=1或q=
+q2,解得q=1或q=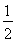 , 4分
, 4分
又由{an}为递减数列,于是q=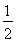 ,
,
∴ an=a1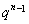 =(
=(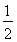 )n. 6分
)n. 6分
(Ⅱ)由于bn=anlog2an=-n?( )n,
)n,
∴  ,
,
于是 ,
,
两式相减得:

∴ 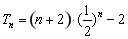 .
.
∴ 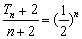 ≥
≥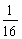 ,解得n≤4,
,解得n≤4,
∴ n的最大值为4. 12分
考点:1.等差数列;2.等比数列的通项公式;3. 错位相消法求和;4.解不等式.


科目:高中数学 来源:2013-2014学年四川绵阳高中高三第二次诊断性考试文科数学试卷(解析版) 题型:解答题
已知首项为 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知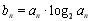 ,求数列{bn}的前n项和
,求数列{bn}的前n项和 .
.
查看答案和解析>>
科目:高中数学 来源:2013年天津市高考数学试卷(理科)(解析版) 题型:解答题
 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.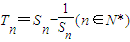 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试文科数学(天津卷解析版) 题型:解答题
已知首项为 的等比数列
的等比数列 的前n项和为
的前n项和为 , 且
, 且 成等差数列.
成等差数列.
(Ⅰ) 求数列 的通项公式;
的通项公式;
(Ⅱ) 证明 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知首项为![]() 的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
(1)求数列{an}的通项公式.
(2)证明Sn+![]() ≤
≤![]() (n∈N*).
(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com