练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．如图，空间四边形OABC中，E，F分别为OA，BC的中点，设$\overrightarrow{OA}$=a，$\overrightarrow{OB}$=b，$\overrightarrow{OC}$=c，试用a，b，c表示$\overrightarrow{EF}$．

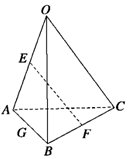
    分析 利用向量的加减法，及线性运算，即可得出结论．

    解答 解：由题意，$\overrightarrow{EF}$=$\overrightarrow{EA}$+$\overrightarrow{AB}$+$\overrightarrow{BF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{a}$+$\frac{1}{2}$（$\overrightarrow{c}$-$\overrightarrow{b}$）=$\frac{1}{2}$（$\overrightarrow{b}$+$\overrightarrow{c}$-$\overrightarrow{a}$）．

    点评 本题考查了平面向量的加减法、线性运算，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．如图，等腰梯形ABCD中，AB∥CD，AD⊥BD，矩形ABEF所在的平面和平面ABCD相互垂直． 
    （1）求证：AD⊥平面DBE；
    （2）若AB=2，AD=AF=1，求三棱锥C-BDE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

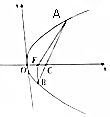    9．如图，设抛物线y2=4x的焦点为F，不经过焦点的直线上有三个不同的点A，B，C，其中点A，B在抛物线上，点C在x轴上，记△BCF的面积为S1，△ACF的面积为S2，则$\frac{{S}_{1}^{2}}{{S}_{2}^{2}}$等于是（　　）
    A．$\frac{{|{BF}|-1}}{{|{AF}|-1}}$B．$\frac{{{{|{BF}|}^2}-1}}{{{{|{AF}|}^2}-1}}$C．$\frac{{|{BF}|+1}}{{|{AF}|+1}}$D．$\frac{{{{|{BF}|}^2}+1}}{{{{|{AF}|}^2}+1}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知实数a满足下列两个条件：
    ①关于x的方程ax2+3x+1=0有解；
    ②代数式log2（a+3）有意义．
    则使得指数函数y=（3a-2）x为减函数的概率为（　　）
    A．$\frac{4}{63}$B．$\frac{1}{16}$C．$\frac{3}{63}$D．$\frac{3}{16}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列四个判断：?
    ①某校高三（1）班的人数和高三（2）班的人数分别是m和n，某次数学测试平均分分别是a，b，则这两个班的数学平均分为$\frac{a+b}{2}$；?
    ②从总体中抽取的样本（1，2.5），（2，3.1），（4，3.9），（5，4.4），则回归直线y=bx+a必过点（3，3.6）；
    ③在频率分布直方图中，众数左边和右边的所有直方图的面积相等．
    其中正确的个数有（　　）
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．数列{an}满足Sn=2n-an（n∈N*）．
    （1）计算a1、a2、a3，并猜想an的通项公式；
    （2）用数学归纳法证明（1）中的猜想．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．下列说法正确的是（　　）
    A．命题“若x2=1，则x=1的否命题为：“若x2=1，则x≠1”
    B．“m=1”是“直线x-my=0和直线x+my=0互相垂直”的充要条件
    C．命题“?x0∈R，使得x02+x0+1＜0”的否定是：“?x∈R，均有x2+x+1＜0”
    D．命题“已知A，B为一个三角形两内角，若A=B，则sinA=sinB”的否命题为真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．过抛物线x2=4y的焦点且与其对称轴垂直的弦AB的长度是（　　）
    A．1B．2C．4D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知双曲线${C_1}：\frac{x^2}{4}-{y^2}=1$，双曲线${C_2}：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点分别为F1，F2，M是双曲线C2的一条渐近线上的点，且OM⊥MF2，O为坐标原点，若${S_{△OM{F_2}}}=16$，且双曲线C1，C2的离心率相同，则双曲线C2的实轴长是（　　）
    A．32B．16C．8D．4

    查看答案和解析>>

    同步练习册答案