
已知函数f(x)= x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较
x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较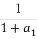 +
+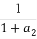 +
+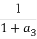 +…+
+…+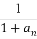 与1的大小,并说明理由.
与1的大小,并说明理由.
见解析
【解析】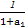 +
+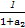 +
+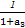 +…+
+…+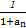 <1.
<1.
理由如下:
∵f'(x)=x2-1,an+1≥f'(an+1),
∴an+1≥(an+1)2-1.
令g(x)=(x+1)2-1,则函数g(x)=x2+2x在区间[1,+∞)上单调递增,于是由a1≥1,得a2≥(a1+1)2-1≥22-1,进而得a3≥(a2+1)2-1≥24-1>23-1,
由此猜想:an≥2n-1.
下面用数学归纳法证明这个猜想:
①当n=1时,a1≥21-1=1,结论成立;
②假设n=k(k≥1且k∈N*)时结论成立,即ak≥2k-1,则当n=k+1时,由g(x)=(x+1)2-1在区间[1,+∞)上单调递增知,ak+1≥(ak+1)2-1≥22k-1≥2k+1-1,即n=k+1时,结论也成立.
由①②知,对任意n∈N*,都有an≥2n-1,
即1+an≥2n,∴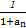 ≤
≤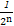 ,
,
∴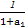 +
+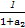 +
+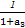 +…+
+…+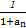 ≤
≤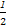 +
+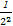 +
+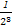 +…+
+…+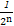 =
=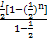 =1-(
=1-(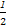 )n<1.
)n<1.
【方法技巧】“归纳——猜想——证明”类问题的一般解题思路
通过观察有限个特例,猜想出一般性的结论,然后用数学归纳法证明.这种方法在解决探索性问题、存在性问题或与正整数有关的命题中有着广泛的应用,其关键是归纳、猜想出公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:填空题
设互不相同的直线l,m,n和平面α,β,γ,给出下列三个命题:
①若l与m为异面直线,l?α,m?β,则α∥β;
②若α∥β,l?α,m?β,则l∥m;
③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
其中真命题的个数为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:填空题
在空间直角坐标系中,以点A(4,1,9),B(10,-1,6),C(x,4,3)为顶点的△ABC是以BC为斜边的等腰直角三角形,则实数x的值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:选择题
已知正方体ABCD-A1B1C1D1中,点E为上底面A1C1的中心,若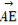 =
=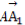 +x
+x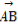 +y
+y ,则x,y的值分别为( )
,则x,y的值分别为( )
(A)x=1,y=1 (B)x=1,y=
(C)x= ,y=
,y= (D)x=
(D)x= ,y=1
,y=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:填空题
若数列{an}的通项公式an=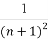 ,记cn=2(1-a1)·(1-a2)…(1-an),试通过计算c1,c2,c3的值,推测cn= .
,记cn=2(1-a1)·(1-a2)…(1-an),试通过计算c1,c2,c3的值,推测cn= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:选择题
用数学归纳法证明不等式1+ +
+ +…+
+…+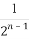 >
>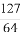 (n∈N*)成立,其初始值至少应取( )
(n∈N*)成立,其初始值至少应取( )
(A)7 (B)8 (C)9 (D)10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:选择题
在证明命题“对于任意角θ,cos4θ-sin4θ=cos2θ”的过程:“cos4θ-sin4θ=(cos2θ+sin2θ)·(cos2θ-sin2θ)=cos2θ-sin2θ=cos2θ”中应用了( )
(A)分析法
(B)综合法
(C)分析法和综合法综合使用
(D)间接证法
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十六第二章第十三节练习卷(解析版) 题型:选择题
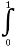 (ex+2x)dx等于( )
(ex+2x)dx等于( )
(A)1 (B)e-1 (C)e (D)e+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com