
分析 (1)利用韦达定理,同角三角的基本关系,求得tan(α+β)的值.
(2)利用同角三角的基本关系,两角和差的三角公式,求得cos(α-β)的值.
解答 解.①由根与系数的关系得:tanα+tanβ=5,tanα•tanβ=6,∴tan(α+β)=$\frac{tanα+tanβ}{1-tanα•tanβ}$=-1.
②由(1)得tanα=2,tanβ=3,或tanα=3,tanβ=2,∴α∈($\frac{π}{3}$,$\frac{π}{2}$)、β∈($\frac{π}{3}$,$\frac{π}{2}$),
∴α+β∈($\frac{2π}{3}$,π ),∴α+β=$\frac{3π}{4}$,∴cos(α+β)=-$\frac{\sqrt{2}}{2}$.
即cos( α+β )=cosαcosβ-sinαsinβ=-$\frac{\sqrt{2}}{2}$.
再根据tanα•tanβ=6,可得sinαsinβ=6cosαcosβ,求得cosαcosβ=$\frac{\sqrt{2}}{10}$,sinαsinβ=$\frac{3\sqrt{2}}{5}$,
∴$cos(α-β)=cosαcosβ+sinαsinβ=\frac{{7\sqrt{2}}}{10}$.
点评 本题主要考查韦达定理,同角三角的基本关系,两角和差的三角公式,属于中档题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
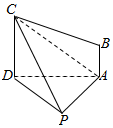 如图,已知平面APD⊥平面ABCD,AB∥CD,CD=AD=AP=4,AB=2,AD⊥AP,CB=2$\sqrt{5}$.
如图,已知平面APD⊥平面ABCD,AB∥CD,CD=AD=AP=4,AB=2,AD⊥AP,CB=2$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
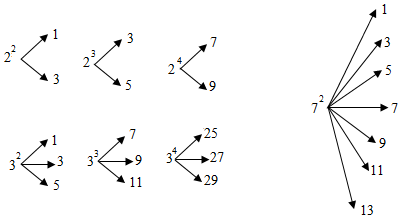 对于mn(m,n∈N且m,n≥2)可以按如下的方式进行“分解”,例如72的“分解“中最小的数是1,最大的数是13.若m3的“分解”中最小的数是111,则m=11.
对于mn(m,n∈N且m,n≥2)可以按如下的方式进行“分解”,例如72的“分解“中最小的数是1,最大的数是13.若m3的“分解”中最小的数是111,则m=11.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com