
定义在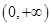 上的函数
上的函数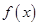 ,如果对任意
,如果对任意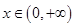 ,恒有
,恒有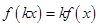 (
(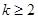 ,
,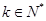 )成立,则称
)成立,则称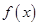 为
为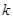 阶缩放函数.
阶缩放函数.
(1)已知函数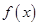 为二阶缩放函数,且当
为二阶缩放函数,且当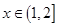 时,
时,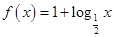 ,求
,求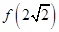 的值;
的值;
(2)已知函数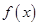 为二阶缩放函数,且当
为二阶缩放函数,且当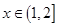 时,
时,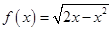 ,求证:函数
,求证:函数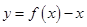 在
在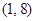 上无零点;
上无零点;
(3)已知函数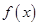 为
为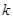 阶缩放函数,且当
阶缩放函数,且当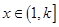 时,
时,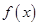 的取值范围是
的取值范围是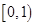 ,求
,求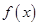 在
在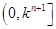 (
(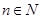 )上的取值范围.
)上的取值范围.
(1)1;(2)详见解析;(3)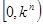 .
.
【解析】
试题分析:(1)本小题首先利用函数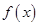 为二阶缩放函数,所以
为二阶缩放函数,所以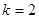 ,于是由
,于是由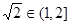 得,
得,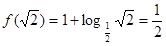 ,由题中条件得
,由题中条件得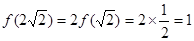 ;
;
(2)本小题首先对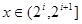
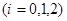 时,
时,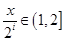 ,得到
,得到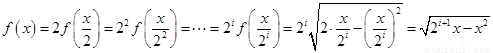 ,方程
,方程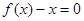
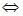
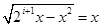
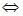
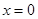 或
或 ,
,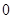 与
与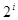 均不属于
均不属于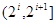 (
(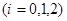 ),所以当
),所以当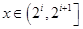
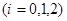 时,方程
时,方程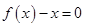 无实数解,所以函数
无实数解,所以函数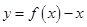 在
在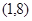 上无零点;
上无零点;
(3)本小题针对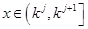 ,
,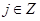 时,有
时,有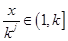 ,依题意可得
,依题意可得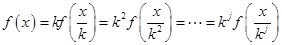 ,然后通过分析可得取值范围为
,然后通过分析可得取值范围为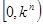 .
.
试题解析:(1)由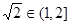 得,
得,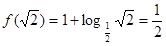 2分
2分
由题中条件得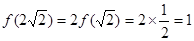 4分
4分
(2)当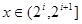
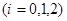 时,
时,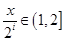 ,依题意可得:
,依题意可得:
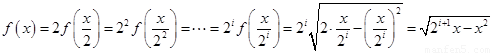 。 6分
。 6分
方程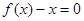
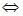
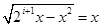
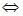
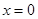 或
或 ,
,
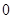 与
与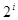 均不属于
均不属于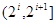 (
(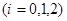 ) 8分
) 8分
当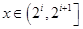 (
(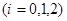 )时,方程
)时,方程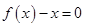 无实数解。
无实数解。
注意到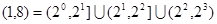 ,所以函数
,所以函数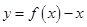 在
在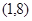 上无零点。 10分
上无零点。 10分
(3)当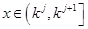 ,
,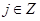 时,有
时,有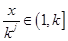 ,依题意可得:
,依题意可得:
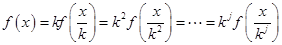
当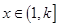 时,
时,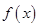 的取值范围是
的取值范围是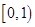 12分
12分
所以当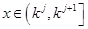 ,
,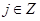 时,
时,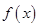 的取值范围是
的取值范围是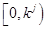 。 14分
。 14分
由于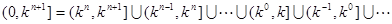 16分
16分
所以函数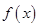 在
在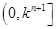 (
(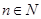 )上的取值范围是:
)上的取值范围是:
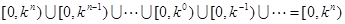 。 18分
。 18分
考点:1.新定义;2.函数的单调性.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源:2015届四川成都七中实验学校高一3月月考数学试卷(解析版) 题型:选择题
定义在 上的函数
上的函数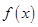 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称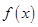 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在 上的如下函数:
上的如下函数:
①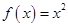 ②
② ③
③ ④
④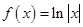
则其中是“保等比数列函数”的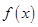 的序号为( )
的序号为( )
A.①② B.③④ C.①③ D.②④
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省东莞市高三第三次月考理科数学试卷(解析版) 题型:选择题
定义在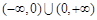 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在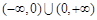 上的如下函数:
上的如下函数:
① ; ②
; ② ; ③
; ③ ; ④
; ④ .
.
则其中是“保等比数列函数”的 的序号为( )
的序号为( )
A.① ② B.③ ④ C.① ③ D.② ④
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(湖北卷解析版) 题型:选择题
定义在 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列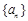 ,
,  仍是等比数列,则称
仍是等比数列,则称 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在 上的如下函数:①
上的如下函数:① ; ②
; ② ; ③
; ③ ; ④
; ④ .则其中是“保等比数列函数”的
.则其中是“保等比数列函数”的 的序号为
的序号为
A、① ② B、③ ④ C、① ③ D、② ④
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试文科数学(湖北卷解析版) 题型:选择题
定义在 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 仍是等比数列,则称
仍是等比数列,则称 为“保等比数列函数”。现有定义在
为“保等比数列函数”。现有定义在 上的如下函数:①
上的如下函数:① ;②
;② ;③
;③ ;④
;④ 。则其中是“保等比数列函数”的
。则其中是“保等比数列函数”的 的序号为
的序号为
A、①② B、③④ C、①③ D、②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com