
【题目】已知正项等比数列{an}的前n项和为Sn , 且S2=6,S4=30,n∈N* , 数列{bn}满足bnbn+1=an , b1=1
(1)求an , bn;
(2)求数列{bn}的前n项和为Tn .
【答案】
(1)解:设正项等比数列{an}的公比为q(q>0),
由题意可得a1+a1q=6,a1+a1q+a1q2+a1q3=30,
解得a1=q=2(负的舍去),
可得an=a1qn﹣1=2n;
由bnbn+1=an=2n,b1=1,
可得b2=2,
即有bn+1bn+2=an=2n+1,
可得 ![]() =2,
=2,
可得数列{bn}中奇数项,偶数项均为公比为2的等比数列,
即有bn=  ;
;
(2)解:当n为偶数时,前n项和为Tn=(1+2+..+ ![]() )+(2+4+..+
)+(2+4+..+ ![]() )
)
= ![]() +
+ ![]() =3(
=3( ![]() )n﹣3;
)n﹣3;
当n为奇数时,前n项和为Tn=Tn﹣1+ ![]()
=3( ![]() )n﹣1﹣3+
)n﹣1﹣3+ ![]() =(
=( ![]() )n+3﹣3.
)n+3﹣3.
综上可得,Tn= ![]()
【解析】(1)设正项等比数列{an}的公比为q(q>0),由等比数列的通项公式,解方程可得首项和公比均为2,可得an=a1qn﹣1=2n;再由n换为n+1,可得数列{bn}中奇数项,偶数项均为公比为2的等比数列,运用等比数列的通项公式,即可得到所求bn;(2)讨论n为奇数和偶数,运用分组求和和等比数列的求和公式,化简整理即可得到所求和.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系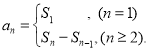 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】某校为了了解学生对消防知识的了解情况,从高一年级和高二年级各选取100名同学进行消防知识竞赛.下图(1)和下图(2)分别是对高一年级和高二年级参加竞赛的学生成绩按![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.

(1)请计算高一年级和高二年级成绩小于60分的人数;
(2)完成下面![]() 列联表,并回答:有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”?
列联表,并回答:有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”?

附:临界值表及参考公式:  ,
, ![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() cos(2x-
cos(2x-![]() ).
).
(1)利用“五点法”,完成以下表格,并画出函数f(x)在一个周期上的图象;
(2)求函数f(x)的单调递减区间和对称中心的坐标;
(3)如何由y=cosx的图象变换得到f(x)的图象.
2x- | 0 |
| π |
| 2π |
x | |||||
f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,面积为![]() 的正方形
的正方形![]() 中有一个不规则的图形
中有一个不规则的图形![]() ,可按下面方法估计
,可按下面方法估计![]() 的面积:在正方形
的面积:在正方形![]() 中随机投掷
中随机投掷![]() 个点,若
个点,若![]() 个点中有
个点中有![]() 个点落入
个点落入![]() 中,则
中,则![]() 的面积的估计值为
的面积的估计值为![]() ,假设正方形
,假设正方形![]() 的边长为2,
的边长为2, ![]() 的面积为1,并向正方形
的面积为1,并向正方形![]() 中随机投掷
中随机投掷![]() 个点,以
个点,以![]() 表示落入
表示落入![]() 中的点的数目.
中的点的数目.

(I)求![]() 的均值
的均值![]() ;
;
(II)求用以上方法估计![]() 的面积时,
的面积时, ![]() 的面积的估计值与实际值之差在区间
的面积的估计值与实际值之差在区间![]() 内的概率.
内的概率.
附表: ![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P 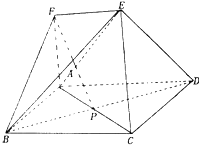
(1)证明:PF∥面ECD;
(2)求二面角B﹣EC﹣A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,命题
,命题![]() ,
,![]() ;命题
;命题![]() .
.
(1)若![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(2)若![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(3)若“![]() ”为假命题,“
”为假命题,“![]() ”为假命题,求
”为假命题,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左右焦点分别为
的左右焦点分别为![]() ,
, ![]() ,左顶点为
,左顶点为![]() ,上顶点为
,上顶点为![]() ,
, ![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,
, ![]() 是线段
是线段![]() 的中点.若经过点
的中点.若经过点![]() 的直线
的直线![]() 与直线
与直线![]() 垂直于点
垂直于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com