
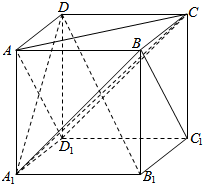
 如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( )
如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由D1C∥A1B,AD1∥BC1,得①正确;由A1D⊥平面ABC1,得②正确;由B1D⊥AD1,B1D⊥AC,得③正确;由M点的轨迹是一条与直线D C1平行的直线,得④错误.
解答 解:在①中:∵在正方体ABCD-A1B1C1D1中,D1C∥A1B,AD1∥BC1,
AD1∩D1C=D1,BC1∩A1B=B,
∴当点P在BC1(不含端点)上运动时,平面AD1C∥平面A1BP,故①正确;
在②中:∵ADD1A1是正方形,∴A1D⊥AD1,
∵AB⊥平面ADD1A1,∴A1D⊥AB,
∵AB∩AD1=A,∴A1D⊥平面ABC1,
∴当点P在BC1(不含端点)上运动时,A1D⊥AP,故②正确;
在③中:∵ADD1A1是正方形,∴A1D⊥AD1,
∵A1B1⊥平面ADD1A1,∴A1D⊥A1B1,
∵A1D∩A1B1=A1,∴AD1⊥平面A1B1D,∴B1D⊥AD1,
同理,B1D⊥AC,又AC∩AD1=A,∴B1D⊥平面ACD1,故③正确;
在④中:M是平面A1B1C1D1上到点D和C1距离相等的点,
∴M点的轨迹是一条与直线D C1平行的直线,而A1D∩D C1=D,故④错误.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com