练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知正项等差数列的前项和为，若，且成等比数列.

    （1）求的通项公式；

    （2）设，记数列的前项和为，求

    【答案】（1）；（2）

    【解析】

    （1）利用等差数列S3=12,等差中项的性质，求得a2=4，结合 2a1，a2，a3+1成等比数列，得a22=2（a2-d）（a2+d+1），进而求得的通项公式；（2）确定数列的通项，利用错位相减法求数列的和.

    设公差为d，则∵S3=12，，即a1+a2+a3=12，∴3a2=12，∴a2=4，

    又∵2a1，a2，a3+1成等比数列，∴a22=2（a2-d）（a2+d+1），解得d=3或d=-4（舍去），

    ∴an=a2+（n-2）d=3n-2

    （2） ，∴ ①

    ①× 得 ②

    ①-②得

    ，

    ∴ ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某市食品药品监督管理局开展2019年春季校园餐饮安全检查，对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分，其评分情况如下表所示：

    中学编号

    1

    2

    3

    4

    5

    6

    7

    8

    原料采购加工标准评分x

    100

    95

    93

    83

    82

    75

    70

    66

    卫生标准评分y

    87

    84

    83

    82

    81

    79

    77

    75

    （1）已知x与y之间具有线性相关关系，求y关于x的线性回归方程；（精确到0.1）

    （2）现从8个被检查的中学食堂中任意抽取两个组成一组，若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分，则组成“对比标兵食堂”，求该组被评为“对比标兵食堂”的概率.

    参考公式：，；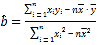

    参考数据：，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大学宣传部组织了这样一个游戏项目：甲箱子里面有3个红球，2个白球，乙箱子里面有1个红球，2个白球，这些球除了颜色以外，完全相同。每次游戏需要从这两个箱子里面各随机摸出两个球.

    （1）设在一次游戏中，摸出红球的个数为，求分布列.

    （2）若在一次游戏中，摸出的红球不少于2个，则获奖.

    ①求一次游戏中，获奖的概率；

    ②若每次游戏结束后，将球放回原来的箱子，设4次游戏中获奖次数为，求的数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，和直线m：，且．

    求a的值；

    是否存在k的值，使直线m既是曲线的切线，又是曲线的切线？如果存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆经过两点，且圆心在直线上．

    （1）求圆的方程；

    （2）已知过点的直线与圆相交截得的弦长为，求直线的方程；

    （3）已知点，在平面内是否存在异于点的定点，对于圆上的任意动点，都有为定值?若存在求出定点的坐标，若不存在说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是：（ ）

    （1）使的值为的赋值语句是；

    （2）用秦九韶算法求多项式在的值时，的值；

    （3）；

    （4）用辗转相除法求得和的最大公约数是.

    A.（1）（2）B.（2）（3）C.（1）（4）D.（2）（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为（为参数），以原点为极点，轴为极轴的极坐标系中，圆的方程．

    （1）写出直线的普通方程和圆的直角坐标方程；

    （2）若点的直角坐标为，圆与直线交于两点，求弦中点的直角坐标和的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A(0，－2)，椭圆E： (a>b>0)的离心率为，F是椭圆E的右焦点，直线AF的斜率为，O为坐标原点.

    (1)求E的方程；

    (2)设过点A的动直线l与E相交于P，Q两点.当△OPQ的面积最大时，求l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若关于的不等式的解集为，求实数的值；

    （2）设，若不等式对都成立，求实数的取值范围；

    （3）若且时，求函数的零点.

    查看答案和解析>>

    同步练习册答案