
ЁОЬтФПЁПвбжЊЮоЧюЪ§Са{an}ЕФИїЯюЖМЪЧе§Ъ§ЃЌЦфЧАnЯюКЭЮЊSn ЃЌ ЧвТњзуЃКa1=aЃЌrSn=anan+1Љ1ЃЌЦфжаaЁй1ЃЌГЃЪ§rЁЪNЃЛ
ЃЈ1ЃЉЧѓжЄЃКan+2ЉanЪЧвЛИіЖЈжЕЃЛ
ЃЈ2ЃЉШєЪ§Са{an}ЪЧвЛИіжмЦкЪ§СаЃЈДцдке§ећЪ§TЃЌЪЙЕУЖдШЮвтnЁЪN* ЃЌ ЖМгаan+T=anГЩСЂЃЌдђГЦ{an}ЮЊжмЦкЪ§СаЃЌTЮЊЫќЕФвЛИіжмЦкЃЌЧѓИУЪ§СаЕФзюаЁжмЦкЃЛ
ЃЈ3ЃЉШєЪ§Са{an}ЪЧИїЯюОљЮЊгаРэЪ§ЕФЕШВюЪ§СаЃЌcn=23nЉ1ЃЈnЁЪN*ЃЉЃЌЮЪЃКЪ§Са{cn}жаЕФЫљгаЯюЪЧЗёЖМЪЧЪ§Са{an}жаЕФЯюЃПШєЪЧЃЌЧыЫЕУїРэгЩЃЌШєВЛЪЧЃЌЧыОйГіЗДР§ЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉжЄУїЃКЁпrSn=anan+1Љ1ЃЌЂй
ЁрrSn+1=an+1an+2Љ1ЃЌЂк
ЂкЉЂйЃЌЕУЃКran+1=an+1ЃЈan+2ЉanЃЉЃЌ
ЁпanЃО0ЃЌЁрan+2Љan=r
ЃЈ2ЃЉНтЃКЕБn=1ЪБЃЌra=aa2Љ1ЃЌЁрa2= ![]() ЃЌ
ЃЌ
ИљОнЪ§СаЪЧИєЯюГЩЕШВюЃЌаДГіЪ§СаЕФЧАМИЯюЃКaЃЌr+ ![]() ЃЌa+rЃЌ2r+
ЃЌa+rЃЌ2r+ ![]() ЃЌa+2rЃЌ3r+
ЃЌa+2rЃЌ3r+ ![]() ЃЌЁЃЎ
ЃЌЁЃЎ
ЕБrЃО0ЪБЃЌЦцЪ§ЯюКЭХМЪ§ЯюЖМЪЧЕЅЕїЕндіЕФЃЌЫљвдВЛПЩФмЪЧжмЦкЪ§СаЃЌ
Ёрr=0ЪБЃЌЪ§СааДГіЪ§СаЕФЧАМИЯюЃКaЃЌ ![]() ЃЌaЃЌ
ЃЌaЃЌ ![]() ЃЌЁЃЎ
ЃЌЁЃЎ
ЫљвдЕБaЃО0ЧвaЁй1ЪБЃЌИУЪ§СаЕФжмЦкЪЧ2
ЃЈ3ЃЉНтЃКвђЮЊЪ§Са{an}ЪЧвЛИігаРэЕШВюЪ§СаЃЌa+a+r=2ЃЈr+ ![]() ЃЉЃЌ
ЃЉЃЌ
ЛЏМђ2a2ЉarЉ2=0ЃЌa= ![]() ЪЧгаРэЪ§ЃЎ
ЪЧгаРэЪ§ЃЎ
Щш ![]() =kЃЌЪЧвЛИіЭъШЋЦНЗНЪ§ЃЌ
=kЃЌЪЧвЛИіЭъШЋЦНЗНЪ§ЃЌ
дђr2+16=k2ЃЌrЃЌkОљЪЧЗЧИКећЪ§r=0ЪБЃЌa=1ЃЌan=1ЃЌSn=nЃЎ
rЁй0ЪБЃЈkЉrЃЉЃЈk+rЃЉ=16=2ЁС8=4ЁС4ПЩвдЗжНтГЩ8зщЃЌ
ЦфжажЛга ![]() ЃЌЗћКЯвЊЧѓЃЌ
ЃЌЗћКЯвЊЧѓЃЌ
ДЫЪБa=2ЃЌan= ![]() ЃЌSn=
ЃЌSn= ![]() ЃЌ
ЃЌ
Ёпcn=23nЉ1ЃЈnЁЪN*ЃЉЃЌan=1ЪБЃЌВЛЗћКЯЃЌЩсШЅЃЎ
an= ![]() ЪБЃЌШє23nЉ1=
ЪБЃЌШє23nЉ1= ![]() ЃЌдђЃК3k=4ЁС3nЉ1Љ1ЃЌn=2ЪБЃЌk=
ЃЌдђЃК3k=4ЁС3nЉ1Љ1ЃЌn=2ЪБЃЌk= ![]() ЃЌВЛЪЧећЪ§ЃЌ
ЃЌВЛЪЧећЪ§ЃЌ
вђДЫЪ§Са{cn}жаЕФЫљгаЯюВЛЖМЪЧЪ§Са{an}жаЕФЯю
ЁОНтЮіЁПЃЈ1ЃЉгЩrSn=anan+1Љ1ЃЌРћгУЕќДњЗЈЕУЃКran+1=an+1ЃЈan+2ЉanЃЉЃЌгЩДЫФмЙЛжЄУїan+2ЉanЮЊЖЈжЕЃЎЃЈ2ЃЉЕБn=1ЪБЃЌra=aa2Љ1ЃЌЙЪa2= ![]() ЃЌИљОнЪ§СаЪЧИєЯюГЩЕШВюЃЌаДГіЪ§СаЕФЧАМИЯюЃЌдйгЩrЃО0КЭr=0СНжжЧщПіНјааЬжТлЃЌФмЙЛЧѓГіИУЪ§СаЕФжмЦкЃЎЃЈ3ЃЉвђЮЊЪ§Са{an}ЪЧвЛИігаРэЕШВюЪ§СаЃЌЫљвдa+a=r=2ЃЈr+
ЃЌИљОнЪ§СаЪЧИєЯюГЩЕШВюЃЌаДГіЪ§СаЕФЧАМИЯюЃЌдйгЩrЃО0КЭr=0СНжжЧщПіНјааЬжТлЃЌФмЙЛЧѓГіИУЪ§СаЕФжмЦкЃЎЃЈ3ЃЉвђЮЊЪ§Са{an}ЪЧвЛИігаРэЕШВюЪ§СаЃЌЫљвдa+a=r=2ЃЈr+ ![]() ЃЉЃЌЛЏМђ2a2ЉarЉ2=0ЃЌНтЕУaЪЧгаРэЪ§ЃЌгЩДЫШыЪжНјааКЯРэВТЯыЃЌФмЙЛЧѓГіSn ЃЎ
ЃЉЃЌЛЏМђ2a2ЉarЉ2=0ЃЌНтЕУaЪЧгаРэЪ§ЃЌгЩДЫШыЪжНјааКЯРэВТЯыЃЌФмЙЛЧѓГіSn ЃЎ
ЁОПМЕуОЋЮіЁПИљОнЬтФПЕФвбжЊЬѕМўЃЌРћгУЪ§СаЕФЭЈЯюЙЋЪНЕФЯрЙижЊЪЖПЩвдЕУЕНЮЪЬтЕФД№АИЃЌашвЊеЦЮеШчЙћЪ§СаanЕФЕкnЯюгыnжЎМфЕФЙиЯЕПЩвдгУвЛИіЙЋЪНБэЪОЃЌФЧУДетИіЙЋЪНОЭНаетИіЪ§СаЕФЭЈЯюЙЋЪНЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2017ФъДКЭэЙ§КѓЃЌЮЊСЫбаОПбндБЩЯДКЭэДЮЪ§гыЪмЙизЂЖШЕФЙиЯЕЃЌФГЭјеОЖдЦфжавЛЮЛОГЃЩЯДКЭэЕФбндБЩЯДКЭэДЮЪ§гыЪмЙизЂЖШНјааСЫЭГМЦЃЌЕУЕНШчЯТЪ§ОнЃК
ЩЯДКЭэДЮЪ§xЃЈЕЅЮЛЃКДЮЃЉ | 2 | 4 | 6 | 8 | 10 |
ЗлЫПЪ§СПyЃЈЕЅЮЛЃКЭђШЫЃЉ | 10 | 20 | 40 | 80 | 100 |
ЃЈ1ЃЉШєИУбндБЕФЗлЫПЪ§СПgЃЈxЃЉЁмgЃЈ1ЃЉ=0гыЩЯДКЭэДЮЪ§xТњзуЯпадЛиЙщЗНГЬЃЌЪдЧѓЛиЙщЗНГЬ ![]() =
= ![]() x+
x+ ![]() ЃЌВЂОЭДЫЗжЮіЃЌИУбндБЩЯДКЭэ12ДЮЪБЕФЗлЫПЪ§СПЃЛ
ЃЌВЂОЭДЫЗжЮіЃЌИУбндБЩЯДКЭэ12ДЮЪБЕФЗлЫПЪ§СПЃЛ
ЃЈ2ЃЉШєгУ ![]() ЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЉБэЪОЭГМЦЪ§ОнЪБЗлЫПЕФЁАМДЪБОљжЕЁБЃЈЫФЩсЮхШыЃЌОЋШЗЕНећЪ§ЃЉЃЌДгет5ИіЁАМДЪБОљжЕЁБжаШЮбЁ2Ъ§ЃЌМЧЫљбЁЕФ2Ъ§жЎКЭЮЊЫцЛњБфСПІЧЃЌЧѓІЧЕФЗжВМСагыЪ§бЇЦкЭћЃЎ ВЮПМЙЋЪНЃК
ЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЉБэЪОЭГМЦЪ§ОнЪБЗлЫПЕФЁАМДЪБОљжЕЁБЃЈЫФЩсЮхШыЃЌОЋШЗЕНећЪ§ЃЉЃЌДгет5ИіЁАМДЪБОљжЕЁБжаШЮбЁ2Ъ§ЃЌМЧЫљбЁЕФ2Ъ§жЎКЭЮЊЫцЛњБфСПІЧЃЌЧѓІЧЕФЗжВМСагыЪ§бЇЦкЭћЃЎ ВЮПМЙЋЪНЃК ![]() =
=  ЃЌ
ЃЌ ![]() =
= ![]() Љ
Љ ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЪЧЖЈвхдк[-1,1]ЩЯЕФЦцКЏЪ§ЃЌЧв
ЪЧЖЈвхдк[-1,1]ЩЯЕФЦцКЏЪ§ЃЌЧв![]() ЃЌШєШЮвтЕФ
ЃЌШєШЮвтЕФ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌзмга
ЪБЃЌзмга![]() ЃЎ
ЃЎ
ЃЈ1ЃЉХаЖЯКЏЪ§![]() дк[-1,1]ЩЯЕФЕЅЕїадЃЌВЂжЄУїФуЕФНсТлЃЛ
дк[-1,1]ЩЯЕФЕЅЕїадЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉНтВЛЕШЪНЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШє![]() ЖдЫљгаЕФ
ЖдЫљгаЕФ![]() КуГЩСЂЃЌЦфжа
КуГЩСЂЃЌЦфжа![]() ЃЈ
ЃЈ![]() ЪЧГЃЪ§ЃЉЃЌЧѓЪЕЪ§
ЪЧГЃЪ§ЃЉЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЖдвЛЧаЪЕЪ§xЁЂyЃЌВЛЕШЪН ![]() Љcos2xЁнasinxЉ
Љcos2xЁнasinxЉ ![]() КуГЩСЂЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
КуГЩСЂЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.ЃЈЉЁоЃЌ ![]() ]
]
B.[3ЃЌ+ЁоЃЉ
C.[Љ2 ![]() ЃЌ2
ЃЌ2 ![]() ]
]
D.[Љ3ЃЌ3]
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЁЭЦНУцBCDЃЌBCЁЭCDЃЌADгыЦНУцBCDЫљГЩЕФНЧЮЊ30ЁуЃЌЧвAB=BC=2ЃЛ 
ЃЈ1ЃЉЧѓШ§РтзЖAЉBCDЕФЬхЛ§ЃЛ
ЃЈ2ЃЉЩшMЮЊBDЕФжаЕуЃЌЧѓвьУцжБЯпADгыCMЫљГЩНЧЕФДѓаЁЃЈНсЙћгУЗДШ§НЧКЏЪ§жЕБэЪОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЮоЧюЪ§Са{an}ЕФИїЯюЖМЪЧе§Ъ§ЃЌЦфЧАnЯюКЭЮЊSn ЃЌ ЧвТњзуЃКa1=aЃЌrSn=anan+1Љ1ЃЌЦфжаaЁй1ЃЌГЃЪ§rЁЪNЃЛ
ЃЈ1ЃЉЧѓжЄЃКan+2ЉanЪЧвЛИіЖЈжЕЃЛ
ЃЈ2ЃЉШєЪ§Са{an}ЪЧвЛИіжмЦкЪ§СаЃЈДцдке§ећЪ§TЃЌЪЙЕУЖдШЮвтnЁЪN* ЃЌ ЖМгаan+T=anГЩСЂЃЌдђГЦ{an}ЮЊжмЦкЪ§СаЃЌTЮЊЫќЕФвЛИіжмЦкЃЌЧѓИУЪ§СаЕФзюаЁжмЦкЃЛ
ЃЈ3ЃЉШєЪ§Са{an}ЪЧИїЯюОљЮЊгаРэЪ§ЕФЕШВюЪ§СаЃЌcn=23nЉ1ЃЈnЁЪN*ЃЉЃЌЮЪЃКЪ§Са{cn}жаЕФЫљгаЯюЪЧЗёЖМЪЧЪ§Са{an}жаЕФЯюЃПШєЪЧЃЌЧыЫЕУїРэгЩЃЌШєВЛЪЧЃЌЧыОйГіЗДР§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВЕФРыаФТЪe= ![]() ЃЌзѓЁЂгвНЙЕуЗжБ№ЮЊF1ЁЂF2 ЃЌ ЖЈЕуЃЌPЃЈ2ЃЌ
ЃЌзѓЁЂгвНЙЕуЗжБ№ЮЊF1ЁЂF2 ЃЌ ЖЈЕуЃЌPЃЈ2ЃЌ ![]() ЃЉЃЌЕуF2дкЯпЖЮPF1ЕФжаДЙЯпЩЯЃЎ
ЃЉЃЌЕуF2дкЯпЖЮPF1ЕФжаДЙЯпЩЯЃЎ
ЃЈЂёЃЉЧѓЭждВCЕФЗНГЬЃЛ
ЃЈЂђЃЉЩшжБЯпlЃКy=kx+mгыЭждВCНЛгкMЁЂNСНЕуЃЌжБЯпF2MЁЂF2NЕФЧуаБНЧЗжБ№ЮЊІСЁЂІТЧвІС+ІТ=ІаЃЌЧѓжЄЃКжБЯпlЙ§ЖЈЕуЃЌВЂЧѓИУЖЈЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩш![]() ЪЧВЛаЁгк3ЕФе§ећЪ§ЃЌМЏКЯ
ЪЧВЛаЁгк3ЕФе§ећЪ§ЃЌМЏКЯ![]() ЃЌЖдгкМЏКЯ
ЃЌЖдгкМЏКЯ![]() жаШЮвтСНИідЊЫи
жаШЮвтСНИідЊЫи![]() ЃЌ
ЃЌ![]() .
.
ЖЈвх1ЃК![]() .
.
ЖЈвх2ЃКШє![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЃЌ
ЃЌ![]() ЛЅЮЊЯрЗДдЊЫиЃЌМЧзї
ЛЅЮЊЯрЗДдЊЫиЃЌМЧзї![]() ЃЌЛђ
ЃЌЛђ![]() .
.
ЃЈЂёЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЪдаДГі
ЃЌЪдаДГі![]() ЃЌ
ЃЌ![]() ЃЌвдМА
ЃЌвдМА![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉШє![]() ЃЌжЄУїЃК
ЃЌжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈЂѓЃЉЩш![]() ЪЧаЁгк
ЪЧаЁгк![]() ЕФе§ЦцЪ§ЃЌжСЩйКЌгаСНИідЊЫиЕФМЏКЯ
ЕФе§ЦцЪ§ЃЌжСЩйКЌгаСНИідЊЫиЕФМЏКЯ![]() ЃЌЧвЖдгкМЏКЯ
ЃЌЧвЖдгкМЏКЯ![]() жаШЮвтСНИіВЛЯрЭЌЕФдЊЫи
жаШЮвтСНИіВЛЯрЭЌЕФдЊЫи![]() ЃЌ
ЃЌ![]() ЃЌЖМга
ЃЌЖМга![]() ЃЌЪдЧѓМЏКЯ
ЃЌЪдЧѓМЏКЯ![]() жадЊЫиИіЪ§ЕФЫљгаПЩФмжЕ.
жадЊЫиИіЪ§ЕФЫљгаПЩФмжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХЃЖйЗЈЧѓЗНГЬfЃЈxЃЉ=0НќЫЦИљдРэШчЯТЃКЧѓКЏЪ§y=fЃЈxЃЉдкЕуЃЈxn ЃЌ fЃЈxnЃЉЃЉДІЕФЧаЯпy=fЁфЃЈxnЃЉЃЈxЉxnЃЉ+fЃЈxnЃЉЃЌЦфгыxжсНЛЕуКсзјБъxn+1=xnЉ ![]() ЃЈnЁЪN*ЃЉЃЌдђxn+1БШxnИќППНќfЃЈxЃЉ=0ЕФИљЃЌЯжвбжЊfЃЈxЃЉ=x2Љ3ЃЌЧѓfЃЈxЃЉ=0ЕФвЛИіИљЕФГЬађПђЭМШчЭМЫљЪОЃЌдђЪфГіЕФНсЙћЮЊЃЈ ЃЉ
ЃЈnЁЪN*ЃЉЃЌдђxn+1БШxnИќППНќfЃЈxЃЉ=0ЕФИљЃЌЯжвбжЊfЃЈxЃЉ=x2Љ3ЃЌЧѓfЃЈxЃЉ=0ЕФвЛИіИљЕФГЬађПђЭМШчЭМЫљЪОЃЌдђЪфГіЕФНсЙћЮЊЃЈ ЃЉ 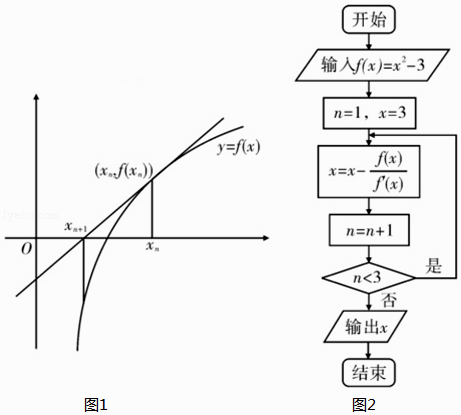
A.2
B.1.75
C.1.732
D.1.73
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com