
【题目】如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且![]() .将角α的终边按逆时针方向旋转
.将角α的终边按逆时针方向旋转![]() ,交单位圆于点B.记A(x1,y1),B(x2,y2).
,交单位圆于点B.记A(x1,y1),B(x2,y2).
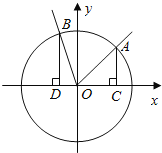
(Ⅰ)若![]() ,求x2;
,求x2;
(Ⅱ)分别过A,B作x轴的垂线,垂足依次为C,D.记△AOC的面积为S1,△BOD的面积为S2.若S1=2S2,求角α的值.
科目:高中数学 来源: 题型:
【题目】某工厂计划出售一种产品,经销人员并不是根据生产成本来确定这种产品的价格,而是通过对经营产品的零售商对于不同的价格情况下他们会进多少货进行调查,通过调查确定了关系式P=-750x+15000,其中P为零售商进货的数量(单位:件),x为零售商支付的每件产品价格(单位:元).现估计生产这种产品每件的材料和劳动生产费用为4元,并且工厂生产这种产品的总固定成本为7000元(固定成本是除材料和劳动费用以外的其他费用),为获得最大利润,工厂应对零售商每件收取多少元?并求此时的最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ex+1)(ax+2a﹣2),若存在x∈(0,+∞),使得不等式f(x)﹣2<0成立,则实数a的取值范围是( )
A.(0,1)
B.(0, ![]() )
)
C.(﹣∞,1)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的长轴长为4,焦距为
的长轴长为4,焦距为![]() .
.
(Ⅰ)求椭圆C的方程;

(Ⅱ)过动点M(0,m)(m>0)的直线交x轴与点N,交C于点A,P(P在第一象限),且M是线段PN的中点,过点P作x轴的垂线交C于另一点Q,延长线QM交C于点B.
(i)设直线PM、QM的斜率分别为k、![]() ,证明
,证明![]() 为定值.
为定值.
(ii)求直线AB的斜率的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a≥3,函数F(x)=min{2|x﹣1|,x2﹣2ax+4a﹣2},其中min(p,q)= ![]()
(1)求使得等式F(x)=x2﹣2ax+4a﹣2成立的x的取值范围
(2)(1)求F(x)的最小值m(a)
(3)求F(x)在[0,6]上的最大值M(a)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com