
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:将函数$f(x)=sin(2x-\frac{π}{3})$的图象向左平移$\frac{π}{3}$个单位,
可得函数y=sin[2(x+$\frac{π}{3}$)-$\frac{π}{3}$]=sin(2x+$\frac{π}{3}$)的图象;
再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
则所得函数图象对应的解析式为g(x)=sin(x+$\frac{π}{3}$),
则g(π)=sin$\frac{4π}{3}$=-$\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,-$\frac{π}{2}$)∪($\frac{π}{3}$,$\frac{π}{2}$) | B. | (-2,-$\frac{π}{2}$) | C. | ($\frac{π}{3}$,$\frac{π}{2}$) | D. | [-2,-$\frac{π}{2}$)∪[$\frac{π}{3}$,$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
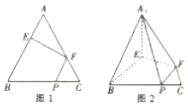 在边长为3的正三角形ABC中,E,F,P分别是AB,AC,BC边上的点,满足$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B,A1P(如图),则以下结论错误的是( )
在边长为3的正三角形ABC中,E,F,P分别是AB,AC,BC边上的点,满足$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B,A1P(如图),则以下结论错误的是( )| A. | CF∥平面A1EP | |
| B. | A1E⊥平面BEP | |
| C. | 点B到面A1PF的距离为$\sqrt{3}$ | |
| D. | 异面直线BP与A1F所成角的余弦值为$\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com