
【题目】已知中心在坐标原点的椭圆 ![]() 的长轴的一个端点是抛物线
的长轴的一个端点是抛物线 ![]() 的焦点,且椭圆
的焦点,且椭圆 ![]() 的离心率是
的离心率是 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)过点 ![]() 的动直线与椭圆
的动直线与椭圆 ![]() 相交于
相交于 ![]() 两点.若线段
两点.若线段 ![]() 的中点的横坐标是
的中点的横坐标是 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】已知线段AB的端点A的坐标为![]() ,端点B是圆
,端点B是圆![]() :
:![]() 上的动点.
上的动点.
(1)求过A点且与圆![]() 相交时的弦长为
相交时的弦长为![]() 的直线
的直线![]() 的方程。
的方程。
(2)求线段AB中点M的轨迹方程,并说明它是什么图形。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司一年需购买某种原料600吨,设公司每次都购买![]() 吨,每次运费为3万元,一年的总存储费为
吨,每次运费为3万元,一年的总存储费为![]() 万元,一年的总运费与总存储费之和为
万元,一年的总运费与总存储费之和为![]() (单位:万元).
(单位:万元).
(1)试用解析式得![]() 表示成
表示成![]() 的函数;
的函数;
(2)当![]() 为何值时,
为何值时, ![]() 取得最小值?并求出
取得最小值?并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,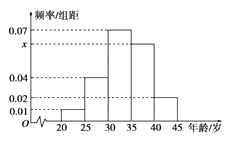
(1)求图中 ![]() 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在 ![]() 岁的人数;
岁的人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为 ![]() ,求
,求 ![]() 的分布列及均值.
的分布列及均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用“斜二测”画法画出△ABC(A为坐标原点,AB在x轴上)的直观图为△A′B′C′,则△A′B′C′的面积与△ABC的面积的比为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com