练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知关于的函数.

    (1)当时，求函数在点处的切线方程；

    (2)设，讨论函数的单调区间；

    (3)若函数没有零点，求实数的取值范围.

    【答案】（1）；（2）见解析；（3）

    【解析】试题分析：(1)当时，得到函数解析式，求得，得到，得出切线的斜率，再利用点斜式求解直线的方程；

    (2)由题意，求出的解析式，求得，可分和两种情况分类讨论，即可求解函数的单调区间；

    (3)由没有零点，转化为方程无解，即与两图象无交点，列出条件，即可求解实数的取值范围.

    试题解析：

    (1)当时， ， ，

    ，∴，即在处的切线方程为.

    (2)∵， ，当时，

    在上恒成立，∴在上单调递增；

    当时，令，解得，

    令，解得，∴在单调递增，在单调递减.

    (3)∵没有零点，

    即无解，∴与两图象无交点，

    设两图象相切于两点，∴，∴， ，∵两图象无交点，∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了实现绿色发展，避免浪费能源，耨市政府计划对居民用电采用阶梯收费的方法.为此，相关部门在该市随机调查了20户居民六月份的用电量（单位：）和家庭收入（单位：万元），以了解这个城市家庭用电量的情况．

    用电量数据如下：18,63,72,82,93,98,106,110,118,130,134,139,147,163,180,194,212,237,260,324．

    对应的家庭收入数据如下：0.21，0.24，0.35,0.40,0.52,0.60,0.58,0.65,0.65,0.63,0.68,0.80,0.83，0.93,0.97,0.96,1.1,1.2,1.5,1.8.

    （1）根据国家发改委的指示精神，该市计划实施3阶阶梯电价，使75%的用户在第一档，电价为0.56元/；的用户在第二档，电价为0.61元/；的用户在第三档，电价为0.86元/；试求出居民用电费用与用电量间的函数关系式；

    （2）以家庭收入为横坐标，电量为纵坐标作出散点图（如图），求关于的回归直线方程（回归直线方程的系数四舍五入保留整数）；

    （3）小明家的月收入7000元，按上述关系，估计小明家月支出电费多少元？

    参考数据：，，，，．

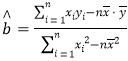    参考公式：一组相关数据的回归直线方程的斜率和截距的最小二乘法估计分别为．，，其中为样本均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个焦点与上、下顶点构成直角三角形，以椭圆的长轴长为直径的圆与直线相切.

    （1）求椭圆的标准方程；

    （2）设过椭圆右焦点且不平行于轴的动直线与椭圆相交于两点，探究在轴上是否存在定点，使得为定值？若存在，试求出定值和点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱中， 、分别是棱、的中点，点在棱上，已知， ， ．

    （1）求证： 平面；

    （2）设点在棱上，当为何值时，平面平面？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了展示中华汉字的无穷魅力，传递传统文化，提高学习热情，某校开展《中国汉字听写大会》的活动．为响应学校号召，2（9）班组建了兴趣班，根据甲、乙两人近期8次成绩画出茎叶图，如图所示（把频率当作概率）．

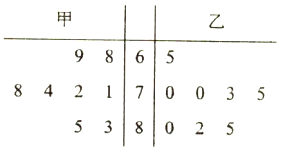
    （1）求甲、乙两人成绩的平均数和中位数；

    （2）现要从甲、乙两人中选派一人参加比赛，从统计学的角度，你认为派哪位学生参加比较合适？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点M是圆心为E的圆上的动点，点，线段MF的垂直平分线交EM于点P.

    （Ⅰ）求动点P的轨迹C的方程；

    （Ⅱ）过原点O作直线交（Ⅰ）中轨迹C于点A、B，点D满足，试求四边形AFBD的面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

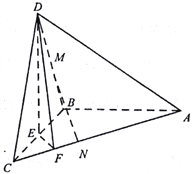
    【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC

    (1)求三棱锥D-ABC的体积

    (2)求证:平面DAC⊥平面DEF;

    (3)若M为DB中点,N在棱AC上,且CN=CA,求证:MN∥平面DEF

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知坐标平面上点与两个定点， 的距离之比等于5.

    （1）求点的轨迹方程，并说明轨迹是什么图形；

    （2）记（1）中的轨迹为，过点的直线被所截得的线段的长为8，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥A-BCDE中，底面BCDE为直角梯形，CD⊥平面ABC，侧面ABC是等腰直角三角形，∠EBC=∠ABC=90°，BC=CD=2BE=2，点M是棱AD的中点

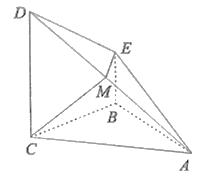
    (I)证明:平面AED⊥平面ACD;

    (Ⅱ)求锐二面角B-CM-A的余弦值

    查看答案和解析>>

    同步练习册答案