
【题目】已知α,β为锐角, ![]() =cos(α+β).
=cos(α+β).
(1)求tan(α+β)cotα的值;
(2)求tanβ的最大值.
【答案】
(1)解:∵sinβ=cos(α+β)sinα,
∴sin[(α+β)﹣α]=cos(α+β)sinα,
∴sin(α+β)cosα﹣cos(α+β)sinα=cos(α+β)sinα
∴sin(α+β)cosα=2cos(α+β)sinα,
∴tan(α+β)cotα=2
(2)解:∵sinβ=cos(α+β)sinα=sinαcosαcosβ﹣sinβsin2α
∴sinβ(1+sin2α)=sinαcosαcosβ,
∴ ![]()
即 ![]() ,
,
∵2tanβtan2α﹣tanα+tanβ=0,
∴(﹣1)2≥4(2tanβ)tanβ,
∴ ![]() ,当且仅当
,当且仅当 ![]() 时等号成立.
时等号成立.
故tanβ的最大值为: ![]()
【解析】(1)由β=(α+β)﹣α,利用三角函数恒等变换的应用即可化简得解.(2)由条件利用两角和差的正弦公式、同角三角函数的基本关系可得2tanβtan2α﹣tanα+tanβ=0,再根据△=1﹣4(2tanβ)tanβ≥0,求得tanβ的最大值.


科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,且其6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,按系统抽样的方法从中抽取一个容量为50的样本,如果在第一组抽得的编号是0015,则在第21组抽得的编号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知α,β∈( ![]() ,π),且sinα+cosα=a,cos(β﹣α)=
,π),且sinα+cosα=a,cos(β﹣α)= ![]() .
.
(1)若a= ![]() ,求sinαcosα+tanα﹣
,求sinαcosα+tanα﹣ ![]() 的值;
的值;
(2)若a= ![]() ,求sinβ的值.
,求sinβ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率. 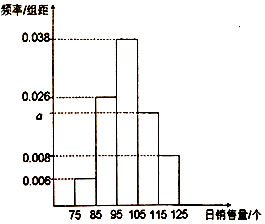
(1)求a的值并估计在一个月(按30天算)内日销售量不低于105个的天数;
(2)利用频率分布直方图估计每天销售量的平均值及方差(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C1:x2+y2=m与圆C2:x2+y2﹣6x﹣8y+16=0相外切.
(1)求m的值;
(2)若圆C1与x轴的正半轴交于点A,与y轴的正半轴交于点B,P为第三象限内一点且在圆C1上,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:四边形ABNM的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形, ![]() .
. 
(1)求证:平面PAM⊥平面PDM;
(2)若点E为PC中点,求二面角P﹣MD﹣E的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com