【题目】下列是合情推理的是（ ）
①由正三角形的性质类比出正三棱锥的有关性质；
②由正方形矩形的内角和是
，归纳出所有四边形的内角和都是；
③三角形内角和是
，四边形内角和是，五边形内角和是
，由此得出凸
边形内角和是
；
④小李某次数学考试成绩是90分，由此推出小李的全班同学这次数学考试的成绩都是90分.
A.①②B.①②③C.①②④D.②③④
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】7人排成一排，按以下要求分别有多少种排法？
(1)甲、乙两人排在一起；
(2)甲不在左端、乙不在右端；
(3)甲、乙、丙三人中恰好有两人排在一起.（答题要求：先列式，后计算）
查看答案和解析>>
科目：高中数学 来源： 题型：
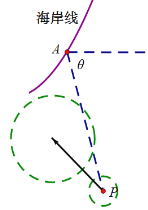
【题目】在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市A（看做一点）的东偏南
角方向
，300 km的海面P处，并以20km / h的速度向西偏北45°方向移动．台风侵袭的范围为圆形区域，当前半径为60 km，并以10km / h的速度不断增大．
（1） 问10小时后，该台风是否开始侵袭城市A，并说明理由；
（2） 城市A受到该台风侵袭的持续时间为多久？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a∈R，函数f（x）=x2﹣2ax+5.
（1）若a>1，且函数f（x）的定义域和值域均为[1，a]，求实数a的值；
（2）若不等式x|f（x）﹣x2|
1对x∈[
，
]恒成立，求实数a的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一次购物抽奖活动中，假设10张奖券中有一等奖奖券1张，可获价值50元的奖品，有二等奖奖券3张，每张可获价值10元的奖品，其余6张没有奖品.
（1）顾客甲从10张奖券中任意抽取1张，求中奖次数X的概率分布；
（2）顾客乙从10张奖券中任意抽取2张，
①求顾客乙中奖的概率；
②设顾客乙获得的奖品总价值Y元，求Y的概率分布及期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某次水下考古活动中,需要潜水员潜入水深为30米的水底进行作业.其用氧量包含3个方面:①下潜时,平均速度为
（米/单位时间）,单位时间内用氧量为
（
为正常数）;②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为
（米/单位时间）, 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为
.
（1）将表示为的函数;
（2）设0<≤5,试确定下潜速度,使总的用氧量最少.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若函数
为定义域
上单调函数，且存在区间
（其中
），使得当
时，的值域恰为
，则称函数是上的正函数，区间叫做等域区间．如果函数
是
上的正函数，则实数
的取值范围为 ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
