
【题目】已知抛物线![]() ,过点
,过点![]() 的直线与抛物线
的直线与抛物线![]() 相切,设第一象限的切点为
相切,设第一象限的切点为![]() .
.
(Ⅰ)证明:点![]() 在
在![]() 轴上的射影为焦点
轴上的射影为焦点![]() ;
;
(Ⅱ)若过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于两点
相交于两点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆且过点
为直径的圆且过点![]() ,求直线
,求直线![]() 与圆
与圆![]() 的方程.
的方程.
【答案】(I)详见解析;(II)详见解析.
【解析】
(Ⅰ)设过点![]() 的直线方程为
的直线方程为![]() ,与抛物线方程联立消元后得到二次方程,根据判别式为零得到
,与抛物线方程联立消元后得到二次方程,根据判别式为零得到![]() ,当
,当![]() 时可求得点
时可求得点![]() 坐标为
坐标为![]() ,而焦点为
,而焦点为![]() ,故结论成立.(Ⅱ)设直线
,故结论成立.(Ⅱ)设直线![]() 的方程为
的方程为![]() ,与抛物线方程联立消元后得到二次方程.由圆
,与抛物线方程联立消元后得到二次方程.由圆![]() 是以线段
是以线段![]() 为直径的圆且过点
为直径的圆且过点![]() 可得
可得![]() ,然后结合根与系数的关系求出
,然后结合根与系数的关系求出![]() 或
或![]() ,进而可得所求方程.
,进而可得所求方程.
(Ⅰ)由题意知可设过点![]() 的直线方程为
的直线方程为![]() ,
,
由![]() 消去
消去![]() 整理得
整理得![]() ,
,
又因为直线与抛物线相切,
所以![]() ,解得
,解得![]() .
.
当![]() 时,直线方程为
时,直线方程为![]() ,可得点
,可得点![]() 坐标为
坐标为![]() ,
,
又因为焦点![]() ,
,
所以点![]() 在
在![]() 轴上的射影为焦点
轴上的射影为焦点![]() .
.
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,
,
由![]() ,
,
其中![]() 恒成立.
恒成立.
设![]() ,
,![]() ,
,
则![]() ,
,
所以![]() ,
,![]() .
.
由于圆![]() 是以线段
是以线段![]() 为直径的圆过点
为直径的圆过点![]() ,则
,则![]() ,
,
所以![]()
所以![]() ,
,
解得![]() 或
或![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)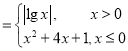 ,g(x)=f(x)-a,
,g(x)=f(x)-a,
(1)讨论函数g(x)的零点个数,并写出相应的实数a的取值范围;
(2)当函数g(x)有四个零点分别为x1,x2,x3,x4时,求x1+x2+x3+x4的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,数列
,数列![]() 满足
满足![]() .
.
![]() Ⅰ
Ⅰ![]() 求数列
求数列![]() 和数列
和数列![]() 的通项公式;
的通项公式;
![]() Ⅱ
Ⅱ![]() 令
令![]() ,若
,若![]() 对于一切的正整数
对于一切的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
![]() Ⅲ
Ⅲ![]() 数列
数列![]() 中是否存在
中是否存在![]() ,且
,且 ![]() 使
使![]() ,
,![]() ,
,![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校2019届高三年级参加市高考模拟考试的学生有1000人,随机抽取了一个容量为200的学生总成绩(满分750分)的样本,各分数段人数如表所示:
分数段 |
|
|
|
|
|
人数 | 20 | 30 | 80 | 40 | 30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)若本次模拟考试一本的预测分数线为550分,试估计该校的一本上线人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次高三年级统一考试中,数学试卷有一道满分为10分的选做题,学生可以从A,B两道题目中任选一题作答,某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名学生的选做题成绩中随机抽取一个容量为10的样本,为此将900名学生的选做题成绩随机编号为001,002,…,900.若采用分层随机抽样,按照学生选择A题目或B题目,将成绩分为两层,且样本中选择A题目的成绩有8个,平均数为7,方差为4;样本中选择B题目的成绩有2个,平均数为8,方差为1.试用样本估计该校900名学生的选做题得分的平均数与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后平均每人每年创造利润为
名员工从事第三产业,调整后平均每人每年创造利润为![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com