
【题目】北京某附属中学为了改善学生的住宿条件,决定在学校附近修建学生宿舍,学校总务办公室用1000万元从政府购得一块廉价土地,该土地可以建造每层1000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高0.02万元,已知建筑第5层楼房时,每平方米建筑费用为0.8万元.
(1)若学生宿舍建筑为![]() 层楼时,该楼房综合费用为
层楼时,该楼房综合费用为![]() 万元,综合费用是建筑费用与购地费用之和),写出
万元,综合费用是建筑费用与购地费用之和),写出![]() 的表达式;
的表达式;
(2)为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
【答案】(1)![]() ;(2)学校应把楼层建成
;(2)学校应把楼层建成![]() 层,此时平均综合费用为每平方米
层,此时平均综合费用为每平方米![]() 万元
万元
【解析】
![]() 由已知求出第
由已知求出第![]() 层楼房每平方米建筑费用为
层楼房每平方米建筑费用为![]() 万元,得到第
万元,得到第![]() 层楼房建筑费用,由楼房每升高一层,整层楼建筑费用提高
层楼房建筑费用,由楼房每升高一层,整层楼建筑费用提高![]() 万元
万元![]() ,然后利用等差数列前
,然后利用等差数列前![]() 项和求建筑
项和求建筑![]() 层楼时的综合费用
层楼时的综合费用![]() ;
;
![]() 设楼房每平方米的平均综合费用为
设楼房每平方米的平均综合费用为![]() ,则
,则![]() ,然后利用基本不等式求最值.
,然后利用基本不等式求最值.
解:![]() 由建筑第5层楼房时,每平方米建筑费用为
由建筑第5层楼房时,每平方米建筑费用为![]() 万元,
万元,
且楼房每升高一层,整层楼每平方米建筑费用提高![]() 万元,
万元,
可得建筑第1层楼房每平方米建筑费用为:![]() 万元.
万元.
建筑第1层楼房建筑费用为:![]() 万元
万元![]() .
.
楼房每升高一层,整层楼建筑费用提高:![]() 万元
万元![]() .
.
建筑第x层楼时,该楼房综合费用为:![]() .
.
![]() ;
;
![]() 设该楼房每平方米的平均综合费用为
设该楼房每平方米的平均综合费用为![]() ,
,
则:![]() ,
,
当且仅当![]() ,即
,即![]() 时,上式等号成立.
时,上式等号成立.
![]() 学校应把楼层建成10层,此时平均综合费用为每平方米
学校应把楼层建成10层,此时平均综合费用为每平方米![]() 万元.
万元.
【点睛】
本题考查简单的数学建模思想方法,训练了等差数列前n项和的求法,训练了利用基本不等式求最值,是中档题.
【题型】解答题
【结束】
20
【题目】已知![]() .
.
(1)求函数![]() 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(2)若![]() ,求
,求![]() 的值域.
的值域.
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的六个命题:
①线性回归直线必过样本数据的中心点![]() ;
;
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于1;
就越接近于1;
⑤残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高;
⑥甲、乙两个模型的![]() 分别约为0.88和0.80,则模型乙的拟合效果更好.
分别约为0.88和0.80,则模型乙的拟合效果更好.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C1上的点均在C2:(x﹣5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(1)求曲线C1的方程
(2)设P(x0 , y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别于曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线 ![]() =1(a,b>0)的两顶点为A1 , A2 , 虚轴两端点为B1 , B2 , 两焦点为F1 , F2 . 若以A1A2为直径的圆内切于菱形F1B1F2B2 , 切点分别为A,B,C,D.则: (Ⅰ)双曲线的离心率e=;
=1(a,b>0)的两顶点为A1 , A2 , 虚轴两端点为B1 , B2 , 两焦点为F1 , F2 . 若以A1A2为直径的圆内切于菱形F1B1F2B2 , 切点分别为A,B,C,D.则: (Ⅰ)双曲线的离心率e=;
(Ⅱ)菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值 ![]() = .
= . 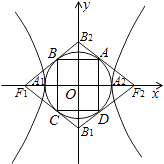
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在送医下乡活动中,某医院安排3名男医生和2名女医生到三所乡医院工作,每所医院至少安排一名医生,且女医生不安排在同一乡医院工作,则不同的分 配方法总数为( )
A.78
B.114
C.108
D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1,F2分别为椭圆C![]()
(1)若椭圆C上的点![]()
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M,N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM,PN的斜率都存在,并记为kPM,kPN时,那么kPM与kPN之积是与点P位置无关的定值,试写出双曲![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4及圆内一点P(2,5).
(1)求过P点的弦中,弦长最短的弦所在的直线方程;
(2)求过点M(5,0)与圆C相切的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com