Question

【题目】已知函数．

（1）若函数在定义域上是单调递增函数，求的取值范围；

（2）若恒成立，求的值．

Answer 1

【答案】（1）；（2）．

【解析】

（1）根据题意，利用导数研究函数的单调性，则在恒成立，可得，方法一：令在恒成立，利用二次函数性质，即可求解参数范围；方法二：令在恒成立，转化不等式，利用基本不等式求解，再根据恒成立思想，即可求解参数取值范围.

（2）由题意，化简得在恒成立，令，不难发现，即在恒成立，根据极值点概念，判断是的极值，可求解参数值，检验成立.

（1）函数在定义域上是单调递增函数，可知导函数在恒成立，

即在恒成立，

可得

方法一：令在恒成立，

①当对称轴，即时，在单调递增，，即恒成立；

②当对称轴，结合二次函数的性质要使在恒成立，，

即，解得

综上可得的取值范围是；

方法二：令在恒成立，

可得

即在恒成立，

，

，

即，

故的取值范围是；

（2）由题意恒成立，

即在恒成立，

令，

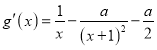
不难发现，即

那么时，取得最大值，也是极大值，

可知是导函数的一个解．

即，

解得

经检验，当时，在递增，在递减，从而成立，符合题意，

故得．