
����Ŀ��κ��ʱ����ѧ��������Ϊ��������������עʱ��������á�IJ�Ϸ��ǡ���������������IJ�Ϸ��ǡ�����ȫ��ͬ���ĸ����湹�ɣ���Ե�����������ͬһԲ���IJ����ϣ�����ͼ�Ͳ���ͼ����Բ��ÿһ��ˮƽ���涼�������Σ����������ۺ�(IJ��)��һ��ķ���ɡ(����)�����ٶ�����ϱ���ʱ����ѧ���敜��ǰ���о��Ļ���������ˡ��敜ԭ�����������Ƽ�ͬ����������족����˼�ǣ����ȸ������壬����ÿһ�ȸߴ��Ľ��������ȣ����������������ȣ���ͼ��һIJ�Ϸ��ǣ�������ͼ�����ͼ���ǰ뾶Ϊ![]() ��Բ��������
��Բ��������![]() ��Ϊ������ֱ���������ĸ����ߣ������敜ԭ������IJ�Ϸ������Ϊ__________��
��Ϊ������ֱ���������ĸ����ߣ������敜ԭ������IJ�Ϸ������Ϊ__________��

���𰸡�![]()
��������
ȡ�����������е�IJ�Ϸ��ǵ�![]() �����о������敜ԭ����֪����������ͬ�ȸ�����������뷽�Dz�(������֮��IJ�Ϸ���֮�ⲿ)�������ȣ��������IJ�Ϸ������.
�����о������敜ԭ����֪����������ͬ�ȸ�����������뷽�Dz�(������֮��IJ�Ϸ���֮�ⲿ)�������ȣ��������IJ�Ϸ������.
ȡ�����������е�IJ�Ϸ��ǵ�![]() �����о������ڸ�Ϊ
�����о������ڸ�Ϊ![]() ����һ��ƽ����������壬������ͼ��Ӱ������ʾ��
����һ��ƽ����������壬������ͼ��Ӱ������ʾ��
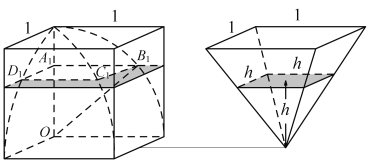

���������ȵȸߵ������Ľ����������Σ��������![]() ��
��
���Dz�(������֮��IJ�Ϸ���֮�ⲿ)�ϵĽ����ǹճ��Σ�������������£�
��![]() ��
��![]() ��
��![]() ��
��
����ͼ����Ӱ�Ĺ������![]() ����Ȼ�������������������
����Ȼ�������������������
�Ӷ����敜ԭ����֪������������뷽�Dz�������ȣ�
���Է��Dz�����Ϊ![]() ��
��
�Ӷ��ɵ�IJ�Ϸ������Ϊ![]() .
.
�ʴ�Ϊ��![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ݺ���![]() ����
����![]() ��
��
��1������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��������![]() ���Ƿ����ʵ��
���Ƿ����ʵ��![]() ʹ��
ʹ��![]() ����СֵΪ0�������ڣ����
����СֵΪ0�������ڣ����![]() ��ֵ���������ڣ�˵�����ɣ�
��ֵ���������ڣ�˵�����ɣ�
��3��������![]() ���Ƿ����ʵ��
���Ƿ����ʵ��![]() ��ʹ����
��ʹ����![]() ��
��![]() �ϵ�ֵ��Ϊ
�ϵ�ֵ��Ϊ![]() �������ڣ����ʵ��
�������ڣ����ʵ��![]() ��ȡֵ��Χ���������ڣ�˵�����ɣ�
��ȡֵ��Χ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ؾ�����ˮ���ý���ˮ�ۣ����Ϊ��ÿ��ÿ����ˮ��������15�ֵIJ��֣�ÿ��3Ԫ������15�ֵ�������25�ֵIJ��֣�ÿ��4.5Ԫ������25�ֵIJ��֣�ÿ��6Ԫ.
��1����ij������ÿ���轻ˮ��![]() ��Ԫ��������ˮ��
��Ԫ��������ˮ��![]() ���֣��ĺ�����ϵʽ��
���֣��ĺ�����ϵʽ��
��2����![]() ������ij�½�ˮ��67.5Ԫ����
������ij�½�ˮ��67.5Ԫ����![]() ��������µ���ˮ����
��������µ���ˮ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ����
����
��1��������ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ʱ���ⲻ��ʽ
ʱ���ⲻ��ʽ![]() ��
��
��3��������ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ����
����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��a��b��0��������
��a��b��0��������![]() ����������Ϊ
����������Ϊ![]() ��
��
��������ԲC�ķ��̣�
������֪A��0��b����B��a��0������P����ԲC��λ�ڵ������Ķ��㣬ֱ��AP��BP�ֱ�x�ᡢy���ڵ�M��N����֤��|AN||BM|Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
�������ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
������������![]() ��
��![]() ��0���������ʵ��
��0���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������![]() ,
,![]() ,
,![]() ������ͬ��������ͬһ��Ʒ������(��λ:��)���±���ʾ.�ʼ���Ա�÷ֲ�����ķ�������Щ��Ʒ�й���ȡ6����Ʒ���м��:
������ͬ��������ͬһ��Ʒ������(��λ:��)���±���ʾ.�ʼ���Ա�÷ֲ�����ķ�������Щ��Ʒ�й���ȡ6����Ʒ���м��:
���� |
|
|
|
���� | 50 | 150 | 100 |
(1)����6����Ʒ������![]() ,
,![]() ,
,![]() �������Ʒ������;
�������Ʒ������;
(2)������6����Ʒ�������ȡ2�����н�һ�����,����2����Ʒ������ͬ����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����sin2x��cos2x��2![]() sinxcosx��x��R��.
sinxcosx��x��R��.
��1����f��x���ĵ����������䣻
��2������f��x��������[![]() ��
��![]() ]�ϵ����ֵ����Сֵ.
]�ϵ����ֵ����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������14�֣���֪����![]() ��
��
����������![]() �ĵ����������䣻
�ĵ����������䣻
������֤������![]() ʱ��
ʱ��![]() ��
��
������ȷ��ʵ��![]() �����п���ȡֵ��ʹ�ô���
�����п���ȡֵ��ʹ�ô���![]() ����
����![]() ʱ������
ʱ������![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com