
【题目】某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A、B、C三地位于同一水平面上,在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,∠BAC=60°,在A地听到弹射声音的时间比在B地晚![]() 秒. A地测得该仪器弹至最高点H时的仰角为30°.
秒. A地测得该仪器弹至最高点H时的仰角为30°.
(1)求A、C两地的距离;
(2)求该仪器的垂直弹射高度CH.(声音的传播速度为340米/秒)

科目:高中数学 来源: 题型:
【题目】已知关于![]() 与
与![]() 有表格中的数据,且
有表格中的数据,且![]() 与
与![]() 线性相关,由最小二乘法得
线性相关,由最小二乘法得![]() .
.
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求![]() 与
与![]() 的线性回归方程;
的线性回归方程;
(2)现有第二个线性模型:![]() ,且
,且![]() .若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由
.若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() 千米,汽车从
千米,汽车从![]() 地匀速行驶到
地匀速行驶到![]() 地,速度不超过
地,速度不超过![]() 千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度
千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度![]() 的平方成正比,比例系数为
的平方成正比,比例系数为![]() ,固定部分为
,固定部分为![]() 元,
元,
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米小时)的函效:并求出当
(千米小时)的函效:并求出当![]() 时,汽车应以多大速度行驶,才能使得全程运输成本最小;
时,汽车应以多大速度行驶,才能使得全程运输成本最小;
(2)随着汽车的折旧,运输成本会发生一些变化,那么当![]() ,此时汽车的速度应调整为多大,才会使得运输成本最小,
,此时汽车的速度应调整为多大,才会使得运输成本最小,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3﹣x2=2.(12分)
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)如图,在平面直角坐标系xOy中,依次连接点P1(x1 , 1),P2(x2 , 2)…Pn+1(xn+1 , n+1)得到折线P1 P2…Pn+1 , 求由该折线与直线y=0,x=x1 , x=xn+1所围成的区域的面积Tn . 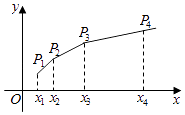
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() .
.

⑴若圆![]() 的半径为2,圆
的半径为2,圆![]() 与
与![]() 轴相切且与圆
轴相切且与圆![]() 外切,求圆
外切,求圆![]() 的标准方程;
的标准方程;
⑵若过原点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中“竹九节”问题曰:“今有竹九节,下三节容量四升,上四节容量三升,问中间两节欲均容各多少?”其意为:“现有一根9节的竹子,自上而下的容积成等差数列,下面3节容量为4升,上面4节容积为3升,问中间2节各多少容积?”则中间2节容积合计________升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com