
【题目】己知函数![]() ,其中
,其中![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)设![]() ,
,![]() ,若存在
,若存在![]() ,对任意的实数
,对任意的实数![]() ,恒有
,恒有![]() 成立,求
成立,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(Ⅰ)求导后讨论![]() 的正负号,即可说明导函数的正负号,即可说明单调性。
的正负号,即可说明导函数的正负号,即可说明单调性。
(Ⅱ)题干等价于存在![]() ,对任意的实数
,对任意的实数![]() ,恒有
,恒有![]() ,记
,记![]() 即讨论
即讨论![]() 的取值,判断
的取值,判断![]() 在
在![]() 的单调性,求出其最小值使
的单调性,求出其最小值使![]() 成立。
成立。
解:(Ⅰ)由题,![]()
(1)当![]() 时,
时,![]() 恒成立,
恒成立,
故此时函数![]() 在
在![]() 上单调递增;
上单调递增;
(2)当![]() 时,函数在
时,函数在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
(Ⅱ)不等式![]()
![]()
记![]() ,
,![]() ,
,
则![]() ,
,
其中![]()
由(Ⅰ)可知函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
(1)若![]() ,则
,则![]() ,
,![]() ,
,
![]() 函数
函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]() ,
,
![]()
(2)若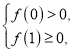 即
即![]() 时,
时,![]() ,
,
![]() 函数
函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
![]() ,
,
![]() ;
;
(3)当![]() 时,此时
时,此时![]() 且
且![]() 在
在![]() 内递减,
内递减,
![]() 在区间
在区间![]() 内有唯一零点,记为
内有唯一零点,记为![]() ,
,
![]() 函数
函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增
上单调递增
从而![]() ,其中
,其中![]()
![]() ,
,
令![]() ,
,![]() ,则
,则![]()
所以![]() ,
,
综上,当![]() 时,
时,![]() 取到最大值为
取到最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】北京市政府为做好![]() 会议接待服务工作,对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测,只有两轮都合格才能进行销售,否则不能销售.已知该海产品第一轮检测不合格的概率为
会议接待服务工作,对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测,只有两轮都合格才能进行销售,否则不能销售.已知该海产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(1)求该海产品不能销售的概率.
(2)如果该海产品可以销售,则每件产品可获利40元;如果该海产品不能销售,则每件产品亏损80元(即获利-80元).已知一箱中有该海产品4件,记一箱该海产品获利![]() 元,求
元,求![]() 的分布列,并求出数学期望
的分布列,并求出数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应市政府迎接全国文明城市创建活动的号召,某学校组织学生举行了文明城市创建知识类竞赛,为了了解本次竞赛中学生的成绩情况,从中抽取![]() 名学生的分数(满分为100分,得分取正整数,抽取学生的分数均在
名学生的分数(满分为100分,得分取正整数,抽取学生的分数均在![]() 之内)作为样本进行统计,按照
之内)作为样本进行统计,按照![]() 分成
分成![]() 组,并作出如下频率分布直方图,已知得分在
组,并作出如下频率分布直方图,已知得分在![]() 的学生有
的学生有![]() 人.
人.

![]() 求频率分布直方图中的的
求频率分布直方图中的的![]() 值,并估计学生分数的众数、平均数和中位数:
值,并估计学生分数的众数、平均数和中位数:
![]() 如果从
如果从![]() 三个分数段的学生中,按分层抽样的方法抽取
三个分数段的学生中,按分层抽样的方法抽取![]() 人参与座谈会,然后再从
人参与座谈会,然后再从![]() 两组选取的人中随机抽取
两组选取的人中随机抽取![]() 人作进一步的测试,求这
人作进一步的测试,求这![]() 人中恰有一人得分在
人中恰有一人得分在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() ,其焦点到准线的距离为2,直线l与抛物线C交于A,B两点,过A,B分别作抛物线C的切线
,其焦点到准线的距离为2,直线l与抛物线C交于A,B两点,过A,B分别作抛物线C的切线![]() ,
,![]() 交于点M
交于点M
(Ⅰ)求抛物线C的方程
(Ⅱ)若![]() ,求三角形
,求三角形![]() 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C.若![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题
均为假命题
D.命题![]() :“
:“![]() ,使得
,使得![]() ”,则非
”,则非![]() :“
:“![]() ,
,![]() ”
”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com