
【题目】方程x2+![]() x-1=0的解可视为函数y=x+
x-1=0的解可视为函数y=x+![]() 的图象与函数y=
的图象与函数y=![]() 的图象交点的横坐标,若x4+ax-4=0的各个实根x1,x2,…,xk(k≤4)所对应的点(xi ,
的图象交点的横坐标,若x4+ax-4=0的各个实根x1,x2,…,xk(k≤4)所对应的点(xi ,![]() )(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .
)(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
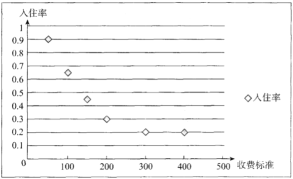
【题目】近年来,随着互联网技术的快速发展,共享经济覆盖的范围迅速扩张,继共享单车、共享汽车之后,共享房屋以“民宿”、“农家乐”等形式开始在很多平台上线.某创业者计划在某景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向,此创业者对该景区附近六家“农家乐”跟踪调查了![]() 天.得到的统计数据如下表,
天.得到的统计数据如下表,![]() 为收费标准(单位:元/日),
为收费标准(单位:元/日),![]() 为入住天数(单位:),以频率作为各自的“入住率”,收费标准
为入住天数(单位:),以频率作为各自的“入住率”,收费标准![]() 与“入住率”
与“入住率”![]() 的散点图如图
的散点图如图
x | 50 | 100 | 150 | 200 | 300 | 400 |
t | 90 | 65 | 45 | 30 | 20 | 20 |
(1)若从以上六家“农家乐”中随机抽取两家深入调查,记![]() 为“入住率”超过
为“入住率”超过![]() 的农家乐的个数,求
的农家乐的个数,求![]() 的概率分布列;
的概率分布列;
(2)令![]() ,由散点图判断
,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(
哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(![]() 结果保留一位小数)
结果保留一位小数)
(3)若一年按![]() 天计算,试估计收费标准为多少时,年销售额
天计算,试估计收费标准为多少时,年销售额![]()
![]() 入住率
入住率![]() 收费标准
收费标准![]() )
)
参考数据: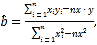
![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为椭圆的右顶点,上顶点和右焦点,且
分别为椭圆的右顶点,上顶点和右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆上的两个动点,若直线
是椭圆上的两个动点,若直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]() ,证明,直线
,证明,直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第16届亚运会在中国广州进行,为了搞好接待工作,组委会招幕了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有![]() 人和
人和![]() 人喜爱运动,其余人不喜爱运动.
人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下![]() 列联表:
列联表:
喜爱运动 | 不喜爱运动 | 总计 | |
男 |
|
| |
女 |
|
| |
总计 |
|
(2)根据列联表的独立性检验,能否在犯错误的概率不超过![]() 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
附:
|
|
|
|
|
|
|
|
|
|
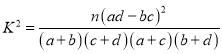 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全国人大第二次会议于2019年3月5日在北京开幕.为广泛了解民意,某人大代表利用网站进行民意调查.数据调查显示,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与调查者中随机选出200人,并将这200人按年龄分组,第1组
.现从参与调查者中随机选出200人,并将这200人按年龄分组,第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
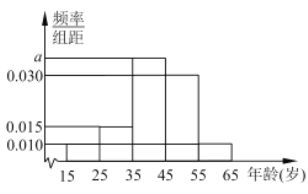
(1)求![]() ;
;
(2)现在要从年龄较小的第1组和第2组中用分层抽样的方法抽取5人,并再从这5人中随机抽取2人接受现场访谈,求这两人恰好属于不同组别的概率;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中不关注民生问题的中老年人有10人,问是否有![]() 的把握认为是否关注民生与年龄有关?
的把握认为是否关注民生与年龄有关?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
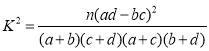 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与平面直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,直线
轴的正半轴重合,直线![]() 的参数方程为
的参数方程为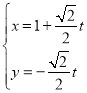 (
(![]() 是参数),曲线
是参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为曲线
为曲线![]() 上一点,求使
上一点,求使![]() 面积取得最大值时的
面积取得最大值时的![]() 点坐标.
点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com