
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,椭圆的一个顶点为
轴上,椭圆的一个顶点为![]() ,右焦点
,右焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,且
,且![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,求四边形
两点,求四边形![]() 的面积的取值范围.
的面积的取值范围.
科目:高中数学 来源: 题型:
【题目】“十三五”规划确定了到2020年消除贫困的宏伟目标,打响了精准扶贫的攻坚战,为完成脱贫任务,某单位在甲地成立了一家医疗器械公司吸纳附近贫困村民就工,已知该公司生产某种型号医疗器械的月固定成本为20万元,每生产1千件需另投入5.4万元,设该公司一月内生产该型号医疗器械x千件且能全部销售完,每千件的销售收入为![]() 万元,已知
万元,已知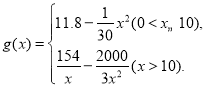
(1)请写出月利润y(万元)关于月产量x(千件)的函数解析式;
(2)月产量为多少千件时,该公司在这一型号医疗器械的生产中所获月利润最大?并求出最大月利润(精确到0.1万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个函数![]() ,如果对任意一个三角形,只要它的三边长
,如果对任意一个三角形,只要它的三边长![]() 、
、![]() 、
、![]() 都在
都在![]() 的定义域内,就有
的定义域内,就有![]() 、
、![]() 、
、![]() 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称![]() 为“保三角形函数”.
为“保三角形函数”.
(1)若![]() 是定义在
是定义在![]() 上的周期函数,且值域为
上的周期函数,且值域为![]() ,证明:
,证明:![]() 不是保三角形函数;
不是保三角形函数;
(2)若![]() 是保三角形函数,求
是保三角形函数,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司新上一条生产线,为保证新的生产线正常工作,需对该生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数![]() ,标准差
,标准差![]() ,绘制如图所示的频率分布直方图,以频率值作为概率估值.
,绘制如图所示的频率分布直方图,以频率值作为概率估值.
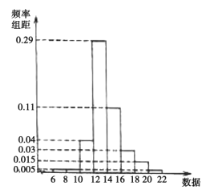
(1)从该生产线加工的产品中任意抽取一件,记其数据为X,依据以下不等式评判(P表示对应事件的概率)
①![]()
②![]()
③![]()
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线,试判断该生产线是否需要检修;
(2)将数据不在![]() 内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为Y,求Y的分布列与数学期望
内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为Y,求Y的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
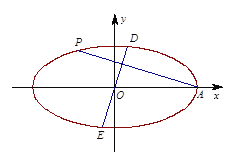
【题目】已知椭圆![]()
![]() 的右顶点
的右顶点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知![]() (异于点
(异于点![]() )为椭圆
)为椭圆![]() 上一个动点,过
上一个动点,过![]() 作线段
作线段![]() 的垂线
的垂线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个三角形的边长与面积都是整数,则称为“海伦三角形”;三边长互质的海伦三角形,称为“本原海伦三角形”;边长都不是3的倍数的本原海伦三角形,称为“奇异三角形”.
(1)求奇异三角形的最小边长的最小值;
(2)求证:等腰的奇异三角形有无数个;
(3)问:非等腰的奇异三角形有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com