
08年陕西卷理)(本小题满分12分)
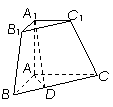
三棱锥被平行于底面![]() 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
科目:高中数学 来源: 题型:
(08年陕西卷理)(本小题满分12分)
已知函数![]() (
(![]() 且
且![]() ,
,![]() )恰有一个极大值点和一个极小值点,其中一个是
)恰有一个极大值点和一个极小值点,其中一个是![]() .
.
(Ⅰ)求函数![]() 的另一个极值点;
的另一个极值点;
(Ⅱ)求函数![]() 的极大值
的极大值![]() 和极小值
和极小值![]() ,并求
,并求![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
08年陕西卷理)(本小题满分12分)
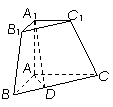
三棱锥被平行于底面![]() 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年陕西卷理)(本小题满分12分)
某射击测试规则为:每人最多射击3次,击中目标即终止射击,第![]() 次击中目标得
次击中目标得![]()
![]() 分,3次均未击中目标得0分.已知某射手每次击中目标的概率为0.8,其各次射击结果互不影响.
分,3次均未击中目标得0分.已知某射手每次击中目标的概率为0.8,其各次射击结果互不影响.
(Ⅰ)求该射手恰好射击两次的概率;
(Ⅱ)该射手的得分记为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com