
分析 (1)由fi(x)=xi(i∈N),求出Fn(x)=(1-x)n,由此能求出F2(1)和F2017(2).
(2)由fi(x)=$\frac{x}{x+i}$(i∈N),知Fn(x)=$\sum_{i=0}^{n}[(-1)^{i}{C}_{n}^{i}\frac{x}{x+i}]$,(n∈N*),由此利用数学归纳法能证明Fn(x)=$\frac{n!}{(x+1)(x+2)…(x+n)}$(n∈N*).
解答 解:(1)∵fi(x)=xi(i∈N),
∴Fn(x)=(-1)0Cn0x0+(-1)1Cn1x1+…+(-1)nCnnxn=(1-x)n,
∴F2(1)=(1-1)2=0,
F2017(2)=(1-2)2017=-1.
证明:(2)∵fi(x)=$\frac{x}{x+i}$(i∈N),
∴Fn(x)=(-1)0Cn0f0(x)+(-1)1Cn1fi(x)+…+(-1)nCnnfn(x)=$\sum_{i=0}^{n}[(-1)^{i}{C}_{n}^{i}\frac{x}{x+i}]$,(n∈N*),
①当n=1时,Fn(x)=$\sum_{i=0}^{1}[(-1)^{i}{C}_{1}^{i}\frac{x}{x+i}]$=1-$\frac{x}{x+1}$=$\frac{1}{x+1}$,∴n=1时,结论成立;
②假设n=k时,结论成立,即Fk(x)=$\sum_{i=0}^{k}[(-1)^{i}{C}_{k}^{i}\frac{x}{x+i}]$=$\frac{k!}{(x+1)(x+2)…(x+k)}$,
则当n=k+1时,Fk+1(x)=$\sum_{i=0}^{k+1}[(-1)^{i}{C}_{k+1}^{i}\frac{x}{x+i}]$
=1+$\sum_{i=1}^{k}[(-1)^{i}{C}_{k+1}^{i}\frac{x}{x+i}]$+(-1)${\;}^{k+1}{C}_{k+1}^{k+1}\frac{x}{x+k+1}$
=$1+\sum_{i=1}^{k}[(-1)^{i}({C}_{k}^{i}+{C}_{k}^{i-1})\frac{x}{x+i}]$+$(-1)^{k+1}{C}_{k+1}^{k+1}\frac{x}{x+k+1}$
=$\sum_{i=0}^{k}[(-1)^{i}{C}_{k}^{i}\frac{x}{x+i}]+\sum_{i=1}^{k+1}[(-1)^{i}{C}_{k}^{i-1}\frac{x}{x+i}]$
=${F}_{k}(x)-\sum_{i=1}^{k+1}[(-1)^{i-1}{C}_{k}^{i-1}\frac{x}{x+i}]$
=${F}_{k}(x)-\sum_{i=0}^{k}[(-1)^{i}{C}_{k}^{i}\frac{x}{x+i+1}]$
=${F}_{k}(x)-\sum_{i=0}^{k}[(-1)^{i}{C}_{k}^{i}\frac{x+1}{x+1+i}]\frac{x}{x+1}$
=${F}_{k}(x)-\frac{x}{x+1}{F}_{k}(x+1)$
=$\frac{k!}{(x+1)(x+2)…(x+k)}$-$\frac{k!}{(x+2)(x+3)…(x+1+k)}•\frac{x}{x+1}$
=$\frac{(x+1+k)•k!-xk!}{(x+1)(x+2)…(x+k)(x+1+k)}$
=$\frac{(k+1)1}{(x+1)(x+2)(x+3)…(x+1+k)}$,
∴n=k+1时,结论也成立.
结合①②知Fn(x)=$\frac{n!}{(x+1)(x+2)…(x+n)}$(n∈N*).
点评 本题考查函数值的求法,考查函数解析式的证明,综合性强,难度大,对数学思维能力要求较高,解题时要注意数学归结法的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2,0) | B. | (0,0,3) | C. | (1,0,3) | D. | (0,2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
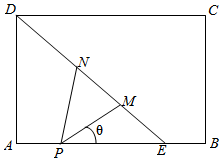 如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方,经测量得知:AD=6米,AE=6米,AP=2米,∠MPN=$\frac{π}{4}$,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米.
如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方,经测量得知:AD=6米,AE=6米,AP=2米,∠MPN=$\frac{π}{4}$,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的图象向左平移π个单位长度可得到y=g(x)的函象 | |
| B. | 函数y=f(x)+g(x)的值域为[-2,2] | |
| C. | 函数y=f(x)•g(x)在$[{0,\frac{π}{2}}]$上单调递增 | |
| D. | 函数y=f(x)-g(x)的图象关于点$({\frac{π}{4},0})$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com